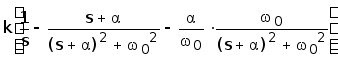Реферат: Дифференцированные уравнения

T₁ =,T₂ ² =-постоянные времени.

Если корни характеристического уравнения для дифференциального уравнения 2-го порядка комплексные (это выполняется при T₁ <2T₂ ), то оно является колебательным. Проверим это для нашего уравнения:

T₁ =0,042

2T₂ =0,14

0,042

Представим данное уравнение в следующем виде:

пусть T₂ =T, .

Тогда уравнение (2):

Здесь T - постоянная времени, x - декремент затухания (0<x<1).

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

(p² +2xTp+1)y(t)=kg(t) (3)

2. Получим передаточную функцию для колебательного звена. Воспользуемся преобразованиями Лапласа:

y(t) = Y(s)

=sY(s)

=s² Y(s)

g(t)=G(s)

По определению передаточная функция находится как отношение выходного сигнала к входному. Тогда уравнение (2) будет иметь вид:

s² Y(s)+2xTsY(s)+Y(s)=kG(s)

W(s)= (4)

3. Найдем выражения для переходной функции и функции веса. По определению аналитическим выражением переходной функции является решение уравнения (2) при нулевых начальных условиях, т.е. g(t)=1 или по преобразованиями Лапласа

h(t)=H(s)

H(s)=W(s)=

Разложив на элементарные дроби правую часть этого выражения, получим

H(s)==

=

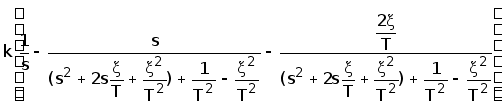
Заменим в этом выражении ,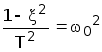.Тогда

H(s)==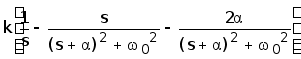

=