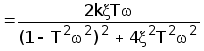Реферат: Дифференцированные уравнения

W(s)=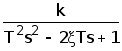 (4)

3. Найдем выражения для переходной функции и функции веса. По определению аналитическим выражением переходной функции является решение уравнения (2) при нулевых начальных условиях, т.е. g(t)=1 или по преобразованиями Лапласа

h(t)=H(s)

H(s)=W(s)=

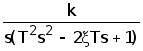
Разложив на элементарные дроби правую часть этого выражения, получим

H(s)==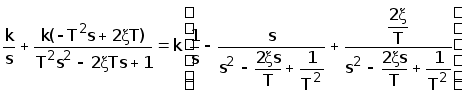

=

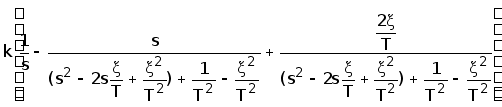
Заменим в этом выражении ,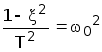.Тогда

H(s)==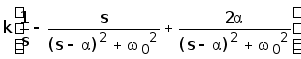

=

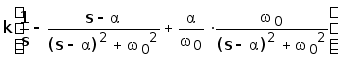
Переходя к оригиналу, получим

h(t)=k =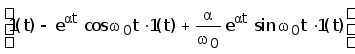

=k Ч1(t)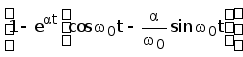 (5)

Функцию веса можно получить дифференцированием переходной функции

w(t)=

или из преобразований Лапласа

w(t)=w(s)

w(s)=W(s)Ч1===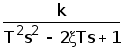

=

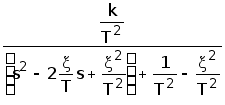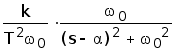
Переходя к оригиналу, получим

w(t)= 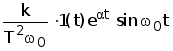(6)

4. Построим графики переходной функции и функции веса. Подставляя исходные данные, вычислим коэффициент передачи, постоянные времени и временные характеристики:

5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw:

W(s)=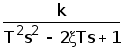

W(jw)= 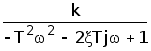(7)

Выделим вещественную и мнимую части :

W(jw)=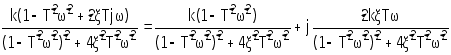

U(w)=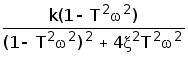

V(w)