Реферат: Дифференцированные уравнения

A(w)=ЅW(jw)Ѕ

A(w)=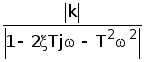= 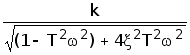(8)

Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.

j(w)=argW(jw)

j(w)=argk - arg(1 - 2xTjw - T² w² )= - arctg

j(w)= - arctg (9)

Для построения логарифмических частотных характеристик вычислим

L(w)=20lg A(w)

L(w)=20lg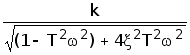

7. Построим графики частотных характеристик. Для этого сначала получим их численные значения.

4.1.5. КОЛЕБАТЕЛЬНОЕ КОНСЕРВАТИВНОЕ ЗВЕНО

1. Данное звено описывается следующим уравнением:

a₂ +a_o y(t) =b_o g(t) (1)

Коэффициенты имеют следующие значения:

a₂ =0,0588

a_o =12

b_o =31,20

Запишем это уравнение в стандартной форме. Для этого разделим (1) на ao:

+y(t)=g(t)

+ y(t)=kg(t) (2),

где k=-коэффициент передачи,

T² =-постоянная времени.

Это уравнение является частным случаем колебательного уравнения при x=0.

Запишем исходное уравнение в операторной форме, используя подстановку p= .Получим:

(T² p² +1)y(t)=kg(t) (3)

2. Получим передаточную функцию для колебательного звена. Воспользуемся преобразованиями Лапласа:

y(t) = Y(s)

=s² Y(s)

g(t)=G(s)