Реферат: Эконометрика 6
2) Нулевая средняя величина остатков. Данная предпосылка всегда выполняется для линейных моделей со свободным коэффициентом b 0 , параметры которых оцениваются обычным методом наименьших квадратов. В нашей модели алгебраическая сумма остатков и, следовательно, их среднее, равны нулю: ![]() (см. прил. 1 ).
(см. прил. 1 ).
Для вычисления суммы и среднего значений остатков использовались встроенные функции EXCEL «СУММ » и «СРЗНАЧ ».
3) Одинаковая дисперсия (гомоскедастичность) остатков. Выполнение данной предпосылки проверим методом Глейзера в предположении линейной зависимости среднего квадратического отклонения возмущений ![]() от предсказанных уравнением регрессии значений результата
от предсказанных уравнением регрессии значений результата ![]() (i =1, 2, …, n ). Для этого рассчитывается коэффициент корреляции
(i =1, 2, …, n ). Для этого рассчитывается коэффициент корреляции ![]() между абсолютными величинами остатков
между абсолютными величинами остатков ![]() и
и ![]() (i =1, 2, …, n ) с помощью выражения, составленного из встроенных функций:
(i =1, 2, …, n ) с помощью выражения, составленного из встроенных функций:
=КОРРЕЛ(ABS(«Остатки »);«Предсказанное Y »)
Коэффициент корреляции оказался равным ![]() (см. прил. 1 ).
(см. прил. 1 ).
Критическое значение коэффициента корреляции для уровня значимости a=0,05 и числа степеней свободы ![]() составляетr кр =0,632.
составляетr кр =0,632.
Так как коэффициент корреляции ![]() не превышает по абсолютной величине критическое значение, то статистическая гипотеза об одинаковой дисперсии остатков не отклоняется на уровне значимости a=0,05.
не превышает по абсолютной величине критическое значение, то статистическая гипотеза об одинаковой дисперсии остатков не отклоняется на уровне значимости a=0,05.
4) Отсутствие автокорреляции в остатках. Выполнение данной предпосылки проверяем методом Дарбина–Уотсона. Предварительно ряд остатков упорядочивается в зависимости от последовательно возрастающих значений результата Y , предсказанных уравнением регрессии. Для этой цели в «Выводе остатка » прил. 1 выделяется любая ячейка в столбце «Предсказанное Y », и на панели инструментов нажимается кнопка «![]() » («Сортировка по возрастанию »). По упорядоченному ряду остатков рассчитываем d ‑статистику Дарбина–Уотсона
» («Сортировка по возрастанию »). По упорядоченному ряду остатков рассчитываем d ‑статистику Дарбина–Уотсона
 (см. прил. 1 ).
(см. прил. 1 ).
Для расчетаd ‑статистики использовалось выражение, составленное из встроенных функций EXCEL:
=СУММКВРАЗН(«Остатки 2, …, n »;«Остатки 1, …, n –1»)/СУММКВ(«Остатки 1, …,n »)
Критические значения d ‑статистики для числа наблюдений n =10, числа факторов p =1 и уровня значимости a=0,05 составляют: d 1 =0,88; d 2 =1,32.
Так как выполняется условие
![]() ,
,
статистическая гипотеза об отсутствии автокорреляции в остатках не отклоняется на уровне значимости a=0,05.
Проверим отсутствие автокорреляции в остатках также и по коэффициенту автокорреляции остатков первого порядка
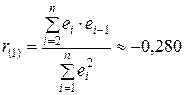 (см. прил. 1 ).
(см. прил. 1 ).
(ряд остатков упорядочен в той же самой последовательности).
Для расчета коэффициента автокорреляции использовалось выражение, составленное из встроенных функций:
=СУММПРОИЗВ(«Остатки 2, …, n »;«Остатки 1, …, n –1»)/СУММКВ(«Остатки 1, …,n »)
Критическое значение коэффициента автокорреляции для числа наблюдений n =10 и уровня значимости a=0,05 составляет r (1)кр =0,632. Так как коэффициент автокорреляции остатков первого порядка не превышает по абсолютной величине критическое значение, то это еще раз указывает на отсутствие автокорреляции в остатках.
5) Нормальный закон распределения остатков. Выполнение этой предпосылки проверяем с помощью R /S -критерия, определяемого по формуле
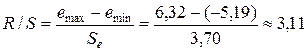 ,
,
где e max =6,32; e min =(–5,19) — наибольший и наименьший остатки соответственно (определялись с помощью встроенных функций «МАКС » и «МИН »);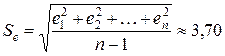 — стандартное отклонение ряда остатков (определено с помощью встроенной функции «СТАНДОТКЛОН ») (см. прил. 1 ).
— стандартное отклонение ряда остатков (определено с помощью встроенной функции «СТАНДОТКЛОН ») (см. прил. 1 ).
Критические границы R / S -критерия для числа наблюдений n =10 и уровня значимости a=0,05 имеют значения: (R /S )1 =2,67 и (R /S )2 =3,69.
Так как расчетное значение R /S -критерия попадает в интервал между критическими границами, то статистическая гипотеза о нормальном законе распределения остатков не отклоняется на уровне значимости a=0,05.
Проведенная проверка показала, что выполняются все пять предпосылок обычного метода наименьших квадратов. Это свидетельствует об адекватности регрессионной модели исследуемому экономическому явлению.
4. Проверим статистическую значимость коэффициентовb 0 и b 1 уравнения регрессии. Табличное значение t -критерия Стьюдента для уровня значимости a=0,05 и числа степеней свободы остатка линейной парной регрессии ![]() составляет t таб =2,306.
составляет t таб =2,306.
t -статистики коэффициентов
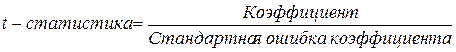 ,
,
были определены при проведении регрессионного анализа в EXCEL и имеют следующие значения: tb 0 »3,202; tb 1 »7,288 (см. прил. 1 ). Анализ этих значений показывает, что по абсолютной величине все они превышают табличное значение t -критерия Стьюдента. Это свидетельствует о статистической значимости обоих коэффициентов. На то же самое обстоятельство указывают и вероятности случайного формирования коэффициентов b 0 и b 1 , которые ниже допустимого уровня значимости a=0,05 (см. «P‑Значение» ).
Статистическая значимость углового коэффициента b 1 дает основание говорить о существенном (значимом) влиянии изменения объема капиталовложений X на изменение объема выпускаемой продукции Y .
5. Коэффициент детерминацииR 2 линейной модели также был определен при проведении регрессионного анализа в EXCEL:
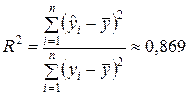
(см. «Регрессионную статистику » в прил. 1 ).
ЗначениеR 2 показывает, что линейная модель объясняет 86,9 % вариации объема выпускаемой продукции Y .