Реферат: Эконометрика 6
F -статистика степенной модели
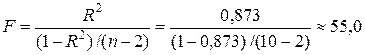
также превышает табличное значениеF -критерия Фишера (F таб =5,32), что указывает на статистическую значимость уравнения степенной регрессии.
Стандартная ошибка степенной регрессии равна
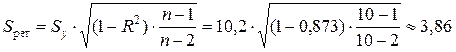млн. руб.
Средняя относительная ошибка аппроксимации имеет значение
.
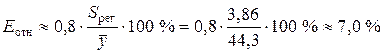Предсказанные уравнением степенной регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 7,0 %. Степенная модель имеет хорошую точность.
3) Показательная (экспоненциальная) модель:
,
где е=2,718… — основание натуральных логарифмов; 
— функция экспоненты (в EXCEL встроенная функция «EXP »).
Параметр b 1 =1,019 является средним коэффициентом роста . Его значение показывает, что при увеличении объема капиталовложений X на 1 млн. руб. объем выпускаемой продукцииY возрастает в среднем в 1,019 раза, то есть на 1,9 %.
Коэффициент детерминации R 2 »0,821 показывает, что показательная модель объясняет 82,1 % вариации объема выпускаемой продукции Y .
F -статистика показательной модели
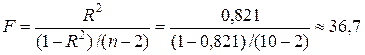
превышает табличное значениеF -критерия Фишера (F таб =5,32), что свидетельствует о статистической значимости уравнения показательной регрессии.
Стандартная ошибка показательной регрессии:
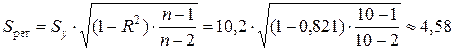млн. руб.
Средняя относительная ошибка аппроксимации:
.
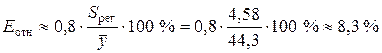Предсказанные уравнением показательной регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 8,3 %. Показательная модель имеет хорошую точность.
Сравнивая между собой коэффициенты детерминации R 2 четырех построенных моделей (линейной, логарифмической, степенной и показательной), можно придти к выводу, что лучшей моделью является логарифмическая модель, так как она имеет самое большое значение R 2 .
ПРИЛОЖЕНИЕ: компьютерные распечатки на 4 листах.
ЗАДАЧА 2
Задача 2а и 2б
Для каждого варианта даны по две структурные формы модели, которые заданы в виде матриц коэффициентов модели. Необходимо записать системы одновременных уравнений и проверить обе системы на идентифицируемость.
| Номер варианта | Номер уравнения | Задача 2а | Задача 2б | ||||||||||||
| переменные | переменные | ||||||||||||||
| у 1 | у 2 | у 3 | х 1 | х 2 | х 3 | x 4 | у 1 | у 2 | у 3 | х 1 | х 2 | х 3 | x 4 | ||
| 11 | 1 | –1 | b 12 | b 13 | a 11 | a 12 | 0 | 0 | –1 | b 12 | b 13 | a 11 | a 12 | 0 | 0 |
| 2 | b 21 | –1 | 0 | a 21 | a 22 | a 23 | 0 | b 21 | –1 | 0 | 0 | a 22 | a 23 | 0 | |
| 3 | b 31 | b 32 | –1 | 0 | 0 | a 3 3 | a 3 4 | b 31 | b 32 | –1 | a 31 | a 32 | 0 | a 3 4 | |
РЕШЕНИЕ
Задача 2а
Используя матрицу коэффициентов модели в исходных данных, записываем систему одновременных уравнений регрессии в структурной форме:
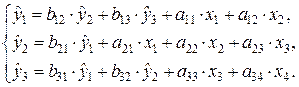
Проверим каждое уравнение системы на выполнение необходимого и достаточного условия идентификации.
В первом уравнении три эндогенные переменные: y 1 ,y 2 иy 3 (H =3). В нем отсутствуют экзогенные переменные x 3 и x 4 (D =2). Необходимое условие идентификации 
выполнено. Для проверки на достаточное условие составим матрицу из коэффициентов при переменных x 3 и x 4 , отсутствующих в данном уравнении, но имеющихся в системе:
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| x 3 | x 4 | |
| 2 | a 23 | 0 |
| 3 | a 33 | a 34 |
Определитель данной матрицы не равен нулю:
,
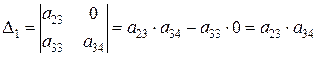а ее ранг равен 2. В заданной системе уравнений три эндогенные переменные —y 1 , y 2 и y 3 . Так как ранг матрицы не меньше, чем количество эндогенных переменных в системе без одного, то достаточное условие идентификации для данного уравнения выполнено. Первое уравнение считается идентифицируемым.
Во втором уравнении две эндогенные переменные: y 1 и y 2 (H =2). В нем отсутствует одна экзогенная переменная x 4 (D =1). Необходимое условие идентификации выполнено. Составим матрицу из коэффициентов при переменных y 3 и x 4 , которые отсутствуют во втором уравнении:
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| y 3 | x 4 | |
| 1 | b 13 | 0 |
| 3 | –1 | a 34 |
Определитель данной матрицы не равен нулю:
,
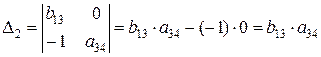а ее ранг равен 2. Значит, достаточное условие идентификации выполнено, и второе уравнение считается идентифицируемым.
В третьем уравнении три эндогенные переменные: y 1 , y 2 и y 3 (H =3). В нем отсутствует экзогенные переменные x 1 и x 2 (D =2). Необходимое условие идентификации выполнено. Составим матрицу из коэффициентов при переменных х 1 и x 2 , которые отсутствуют в третьем уравнении:
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| x 1 | x 2 | |
| 1 | a 11 | a 12 |
| 2 | a 21 | a 22 |
Определитель данной матрицы равен
,
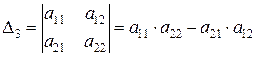