Реферат: Эконометрика 6

(см. «Дисперсионный анализ » в прил. 1 ).

Табличное значениеF -критерия Фишера для уровня значимости a=0,05 и чисел степеней свободы числителя (регрессии) и знаменателя (остатка) составляетF _таб =5,32. Так как F -статистика превышает табличное значениеF -критерия Фишера, то это свидетельствует о статистической значимости уравнения регрессии в целом. На этот же факт указывает и то, что вероятность случайного формирования уравнения регрессии в том виде, в каком оно получено, составляет 8,49×10^-5 (см. «Значимость F » в «Дисперсионном анализе » прил. 1 ), что ниже допустимого уровня значимости a=0,05.

Среднюю относительную ошибку аппроксимации определяем по приближенной формуле

,

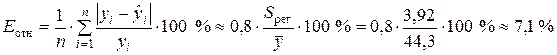где млн. руб. — средний объем выпускаемой продукции, определенный с помощью встроенной функции «СРЗНАЧ » (см. «Исходные данные » в прил. 1 ).

Значение Е _отн показывает, что предсказанные уравнением регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 7,1 %. Линейная модель имеет хорошую точность.

По результатам проверок, проведенных в пунктах 3 — 5, можно сделать вывод о достаточно хорошем качестве линейной модели и возможности ее использования для целей анализа и прогнозирования объема выпускаемой продукции.

6. Спрогнозируем объем выпускаемой продукции Y , если прогнозное значение объема капиталовложений X составит 80 % от своего максимального значения в исходных данных:

- максимальное значение X —x _max =59 млн. руб. (см. «Исходные данные » в прил. 1 );

- прогнозное значение X — млн. руб.

Среднее прогнозируемое значение объема выпускаемой продукции (точечный прогноз ) равно

млн. руб.

Стандартная ошибка прогноза фактического значенияобъема выпускаемой продукцииy ₀ рассчитывается по формуле

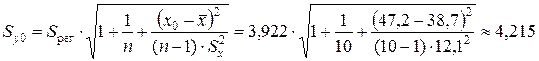млн. руб.,

где млн. руб. — средний объем капиталовложений; млн. руб. — стандартное отклонение объема капиталовложений (определены с помощью встроенных функций «СРЗНАЧ » и «СТАНДОТКЛОН ») (см. «Исходные данные » в прил. 1 ).

Интервальный прогноз фактического значения объема выпускаемой продукцииy ₀ с надежностью (доверительной вероятностью) g=0,9 (уровень значимости a=0,1) имеет вид:

млн. руб.,

гдеt _таб =1,860 — табличное значение t -критерия Стьюдента при уровне значимости a=0,1 и числе степеней свободы .

Таким образом, объем выпускаемой продукции Y с вероятностью 90 % будет находиться в интервале от 43,2 до 58,8 млн. руб.

7. График, на котором изображены фактические и предсказанные уравнением регрессии значения Y строим с помощью диаграммы EXCEL (меню «Вставка» ® «Диаграмма… » ® «Точечная »). Далее строим линию линейного тренда (меню «Диаграмма» ® «Добавить линию тренда… » ® «Линейная »), и устанавливаем вывод на диаграмме уравнения регрессии и коэффициента детерминации R ² :

Точки точечного и интервального прогнозов наносим на график вручную (прил. 3 ).

8. Логарифмическую, степенную и показательную модели также строим с помощью диаграммы EXCEL (меню «Вставка» ® «Диаграмма… » ® «Точечная »). Далее последовательно строим соответствующие линии тренда (меню «Диаграмма» ® «Добавить линию тренда… »), и устанавливаем вывод на диаграмме уравнения регрессии и коэффициента детерминации R ² :

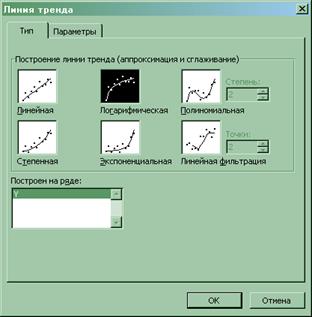
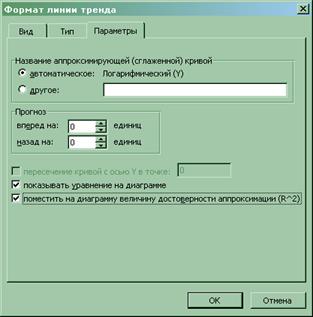
Графики линий регрессии, уравнения регрессии и значения R ² приведены в прил. 4 . Рассмотрим последовательно каждую модель.

1) Логарифмическая модель :

.

Значение параметра b ₁ =29,9 показывает, что при увеличении объема капиталовложений X на 1 % объем выпускаемой продукцииY возрастает в среднем на млн. руб.

Коэффициент детерминации R ² »0,898 показывает, что логарифмическая модель объясняет 89,8 % вариации объема выпускаемой продукции Y .

F -статистика Фишера логарифмической модели определяется через коэффициент детерминации R ² по формуле

.

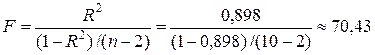Табличное значениеF -критерия Фишера одинаково как для линейной, так и для всех нелинейных моделей, которые здесь строятся (F _таб =5,32). Так как F -статистика превышает табличное значениеF -критерия, то это свидетельствует о статистической значимости уравнения логарифмической регрессии.

Стандартная ошибка логарифмической регрессии также рассчитывается через коэффициент детерминации R ² по формуле

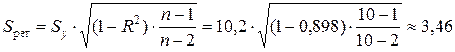млн. руб.,

где млн. руб. — стандартное отклонение объема выпускаемой продукции, определенное с помощью встроенной функции «СТАНДОТКЛОН » (см. «Исходные данные » в прил. 1 ).

Среднюю относительную ошибку аппроксимации определяем по приближенной формуле

.

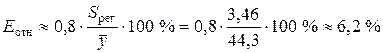Предсказанные уравнением логарифмической регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 6,2 %. Логарифмическая модель имеет хорошую точность.

2) Степенная модель:

.

Показатель степени b ₁ =0,721 является средним коэффициентом эластичности . Его значение показывает, что при увеличении объема капиталовложений X на 1 % объем выпускаемой продукцииY возрастает в среднем на 0,721 %.