Реферат: Эконометрика 6

Таким образом, все три уравнения заданной системы идентифицируемы, а значит, идентифицируема и вся система в целом.

Задача 2б

Используя матрицукоэффициентов модели в исходных данных, записываем систему одновременных уравнений регрессии в структурной форме:

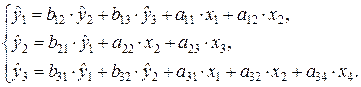
Проверим каждое уравнение системы на выполнение необходимого и достаточного условия идентификации.

В первом уравнении три эндогенные переменные: y ₁ ,y ₂ иy ₃ (H =3). В нем отсутствуют экзогенные переменные x ₃ и x ₄ (D =2). Необходимое условие идентификации выполнено. Для проверки на достаточное условие составим матрицу из коэффициентов при переменных x ₃ и x ₄ , отсутствующих в данном уравнении, но имеющихся в системе:

Уравнения, из которых взяты коэффициенты при переменных	Переменные
	x 3	x 4
2	a 23	0
3	0	a 34

Определитель матрицы не равен нулю:

,

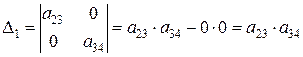а ее ранг матрицы равен 2. В заданной системе уравнений три эндогенные переменные —y ₁ , y ₂ и y ₃ . Так как ранг матрицы не меньше, чем количество эндогенных переменных в системе без одного, то достаточное условие идентификации для данного уравнения выполнено. Первое уравнение считается идентифицируемым.

Во втором уравнении две эндогенные переменные: y ₁ и y ₂ (H =2). В нем отсутствует экзогенные переменные x ₁ и x ₄ (D =2). Так как , то это означает, что данное уравнение сверхидентифицируемо.

В третьем уравнении три эндогенные переменные: y ₁ , y ₂ и y ₃ (H =3). В нем отсутствует одна экзогенная переменная x ₃ (D =1). Так как , то это означает, что данное уравнение неидентифицируемо.

Таким образом, первое уравнение заданной системы идентифицируемо, второе — сверхидентифицируемо, а третье — неидентифицируемо. Если хотя бы одно уравнение системы неидентифицируемо, то вся система считается неидентифицируемой. Данная система является неидентифицируемой и не имеет статистического решения.

Задача 2в

По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов, построить структурную форму модели вида:

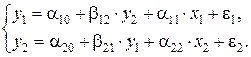
Вариант	n	у 1	у 2	х 1	х 2
11	1	33,0	37,1	3	11
	2	45,9	49,3	7	16
	3	42,2	41,6	7	9
	4	51,4	45,9	10	9
	5	49,0	37,4	10	1
	6	49,3	52,3	8	16

РЕШЕНИЕ

С помощью табличного процессора EXCELстроим два приведенных уравнения системы одновременных уравнений регрессии (меню «Сервис» ® «Анализ данных… » ® «Регрессия »):

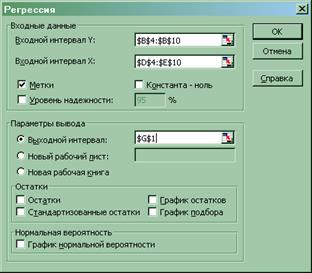
Данные уравнения образуют приведенную форму системы одновременных уравнений регрессии:

Коэффициенты приведенной формы имеют следующие значения:d ₁₀ »19,90; d ₁₁ »2,821; d ₁₂ »0,394; d ₂₀ »19,14; d ₂₁ »1,679 и d ₂₂ »1,181 (см. прил. ).

Таким образом, приведенная форма системы уравнений имеет вид:

Определим коэффициенты структурной формы системы уравнений

Структурные коэффициенты определяются по формулам:

;

;

;

;

;

.

Окончательно структурная форма системы одновременных уравнений регрессии примет вид:

ПРИЛОЖЕНИЕ: компьютерная распечатка на 1 листе.