Реферат: Экономико-статистический анализ эффективности производства зерна Зуевского и Оричевского районов

2) Для характеристики меры рассеяния признака определяют показатели вариации: размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Размах вариации составит: R = x_max – x_min = 28,6 – 6,3 = 25,5 (ц/га)

Дисперсия определяется по формуле

Среднее квадратическое отклонение признака в ряду распределения составит:

(ц/га).

Для определения коэффициента вариации используем формулу

3) Для характеристики формы распределения могут быть использованы коэффициенты асимметрии (А_s ) и эксцесса (Е_s ):

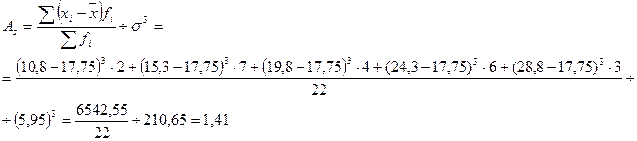
Т.к. >0, распределение имеет правостороннюю асимметрию, о которой также можно судить на основе следующего неравенства: <<

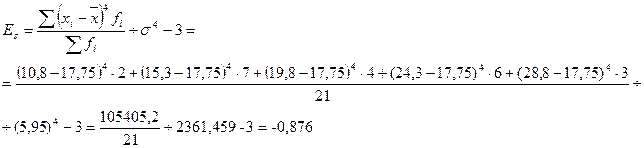Т.к. E_s <0, распределение является низковершинным по сравнению с нормальным.

Для того чтобы определить подчиняется ли эмпирическое (исходное) распределение закону нормального распределения, необходимо проверить статистическую гипотезу о существенности различия частот фактического и теоретического (нормального) распределения.

Наиболее часто для проверки таких гипотез используют критерий Пирсона (χ² ), фактическое значение которого определяют по формуле

где f_i и f_m – частоты фактического и теоретического распределения.

Теоретические частоты для каждого интервала определим в следующей последовательности:

1) Для каждого интервала определим нормированное отклонение (t):

Например, для первого интервала и т.д.

Результаты расчета значений t представим в таблице 9.

2) Используя математическую таблицу “Значения функции 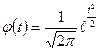” , при фактической величине t для каждого интервала найдем значение функции нормального распределения (таблица 9).

3) Определим теоретические частоты по формуле f_{m =} ,

где n – число единиц в совокупности;

h – величина интервала.

n = 21, h= 5,1, σ = 6,971

Таблица 9 – Эмпирическое и теоретическое распределение предприятий по

урожайности зерновых

Срединное значение интервала по урожайности,ц	Число хозяйств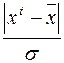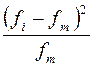
	fi	t	табличное	fm	-
7,45	6	1,11	0,2155	4	1,00
12,55	6	0,38	0,3712	6	0,00
14,65	4	0,35	0,3752	6	0,67
22,75	2	1,08	0,2227	4	1,00
27,85	3	1,81	0,0775	1	4,00
Итого	21	x	x	21	6,67

4) Подсчитаем сумму теоретических частот и проверим ее равенство фактическому числу единиц, т.е..(21=21)

Таким образом, фактическое значение критерия составило =6,67.

По математической таблице “Распределение χ² ” определяем критическое значение критерия χ² при числе степеней свободы (ν) равном числу интервалов минус единица и выбранном уровне значимости (в экономических исследованиях чаще всего используют уровень значимости равный 0,05). При ν = 5 – 1 = 4 и α=0,05 =9,95