Реферат: Электростатика
В соответствии с (7), поток вектора напряжённости сквозь сферическую поверхность радиуса R, охватывающую сферический заряд q, находившийся в её центре:
(Рисунок)
(10)
Этот результат справедлив для замкнутой поверхности любой формы. Рассмотрим общий случай для произвольной поверхности, окружающей n зарядов.
В соответствии с принципом суперпозиции 
. Поэтому 
,
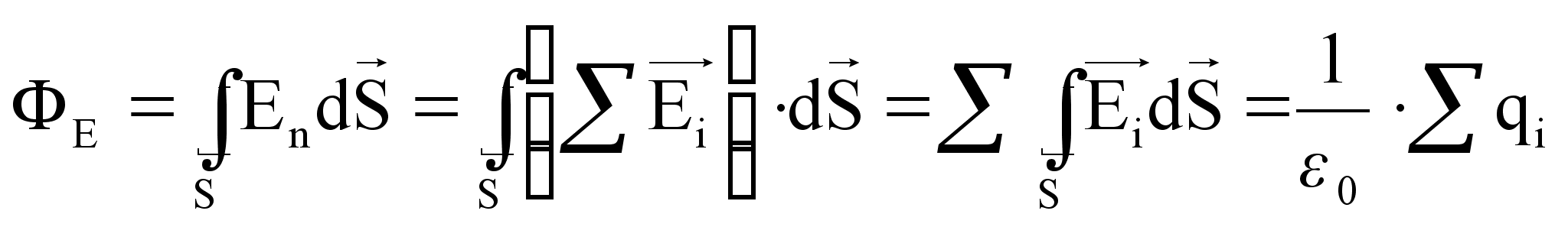(11)
(11) – выражает теорему Гаусса для электростатического поля:
Поток вектора напряжённости электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключённых внутри этой поверхности зарядов, делённых на электрическую постоянную.
Если заряд распределён с объёмной плотностью 
, то
(12)
или 
(13)
Применение теоремы Гаусса к расчёту поля.
-
Поле равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда
.
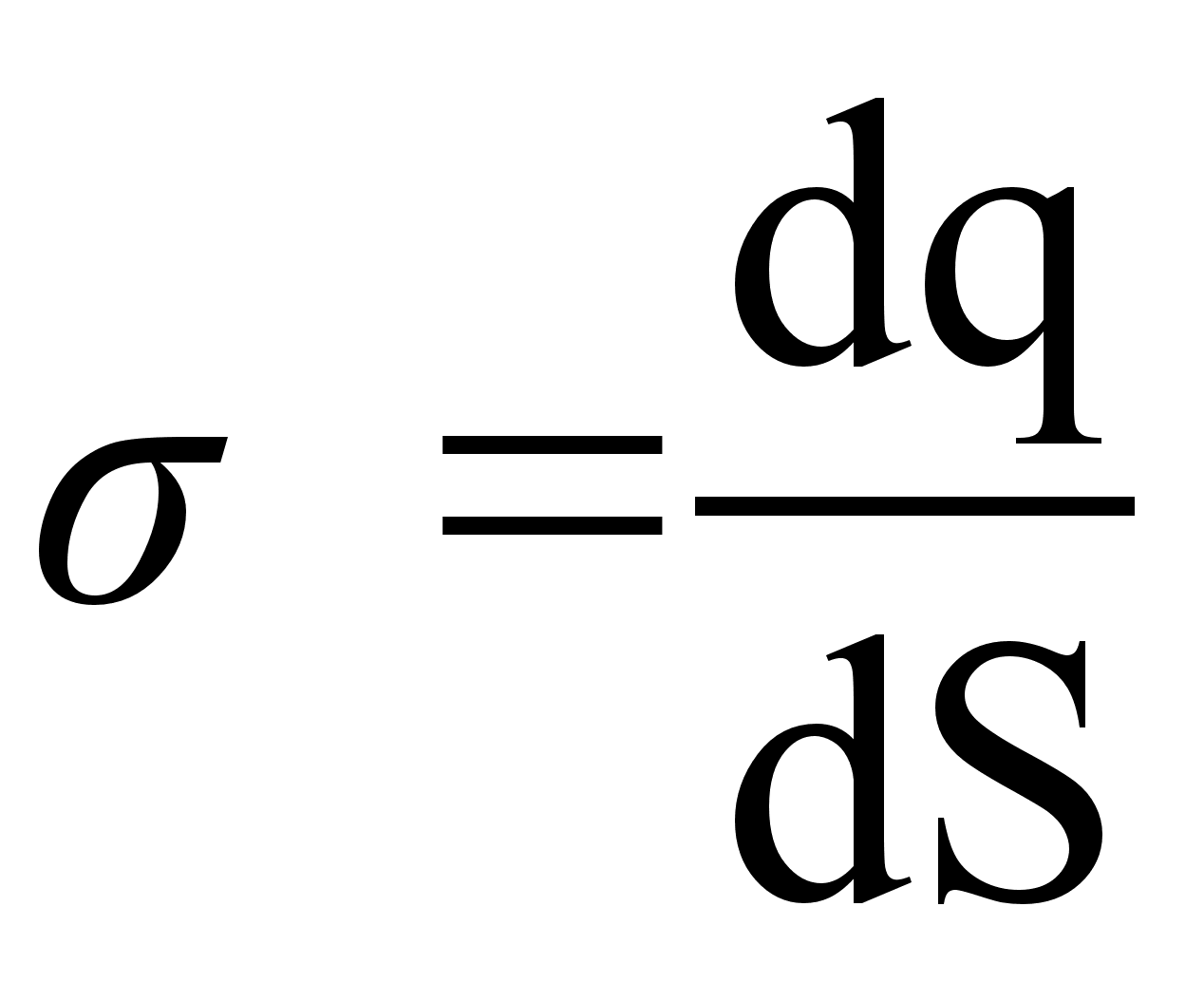(Рисунок)
В качестве замкнутой поверхности возьмём цилиндр, ось которого перпендикулярна плоскости. Поток через боковые стенки цилиндра равен нулю, так как линии напряжённости перпендикулярны оси цилиндра и его образующей. Полный поток сквозь цилиндр равен сумме потоков через его основания 
.
Заряд внутри цилиндра согласно теореме Гаусса:
, откуда 
.
-
Поле равномерно заряженной сферической поверхности.
(Рисунок)
Если r >R, то по теореме Гаусса получим:
, где
, откуда 
.
Если 
< R, то замкнутая поверхность не содержит электрического заряда. Следовательно E = 0.
Дивергенция и ротор электростатического поля.
Заменяя по теореме Гаусса поверхностный интеграл объёмным, получим:
Подставив вместо 
его значение из (13), получим:
Интегралы равны, следовательно равны и подынтегральные выражения. Так получим теорему Гаусса для вектора напряжённости электростатического поля: