Реферат: Фильтрация газов(баротермический эффект)

Полная потенциальная энергия ван-дер-ваальсовых сил описывается суммой:

U = Uор + Uинд + Uдисп .

(I.1.1)

Для полярных молекул основную роль играют ориентационные силы притяжения, для остальных молекул – дисперсионные силы. Энергия ван-дер-ваальсового притяжения составляет (0,1 – 1) ккал/моль [7]. В большинстве случаев ван-дер-ваальсовы силы притяжения перекрываются значительно превосходящими их химическими валентными силами притяжения с энергиями порядка (10 – 100) ккал/моль.

Согласно упрощенной модели ван-дер-ваальсовых сил, молекулы газа – абсолютно упругие шары – притягиваются с силами, достигающими наибольшего значения при непосредственном их соприкосновении. Силы отталкивания проявляют себя на значительно меньших расстояниях.

Для описания свойств реальных газов применяют различные уравнения состояния, отличные от уравнения Клапейрона-Менделеева. Наиболее удобны двухпараметрические уравнения, разрешимые относительно давления и содержащие объем в третьей степени (кубические уравнения состояния). Первое такое уравнение было предложено Ван-дер-Ваальсом в 1873 г.

Уравнение Ван-дер-Ваальса состояния реального газа имеет следующий вид [7]:

,

(I.1.2)

где V₀ – объем 1 моля газа, а – внутреннее давление , обусловленное силами притяжения между молекулами, b – поправка за собственный объем молекул, учитывающая действие сил отталкивания между молекулами и равная учетверенному объему молекул в 1 моле газа:

,

(I.1.3)

.

(I.1.4)

Здесь N_A – число Авогадро, d – диаметр молекулы, U(r) – потенциальная энергия притяжения двух молекул.

Уравнение состояния Бертло (1900г.) :

.

(I.1.5)

Здесь а и b связаны с параметрами критического состояния (в критической точке) соотношениями [8]:

.

(I.1.6)

Уравнение состояния Вукаловича и Новикова [7]:

.

(I.1.7)

Здесь B₁ , B₂ и т.д. – так называемые вириальные коэффициенты весьма сложного вида. Их вычисление производится с учетом ассоциации молекул – объединения под влиянием ван-дер-ваальсовых сил притяжения.

Уравнение состояния Майера [7]:

,

(I.1.8)

где: dt_i =dq_i1 *...dq_in.

Здесь U_{п ij} – взаимная потенциальная энергия i-й и j-й молекул, взаимодействующих по закону центральных сил, q_{i 1} ,......,q_in – обобщенные координаты i-той молекулы, обладающей n степенями свободы.

Уравнение Камерлинг-Оннеса (1901) [8]:

(I.1.9)

где , .

Уравнение Редлиха-Квонга (1949 г.) [8]:

(I.1.10)

Здесь 0,42748·R² ·T^2,5 _k /P_k , b = 0,08664·R·T_k /P_k . Уравнение Редлиха-Квонга считается наилучшим двухконстантным уравнением. При его выводе авторы не руководствовались какими-то определенными теоретическими обоснованиями [8]. Это уравнение следует рассматривать как произвольную, но удачную эмпирическую модификацию предшествующих уравнений состояния.

Уравнение Мартина (1967 г.) [8]:

,

(I.1.11)

где 27·R² ·T² _k /(64P_k ), b = R·T_k /(8P_k ).

1.2. Основные уравнения, описывающие процесс фильтрации газа в пористой среде

В последнее время наблюдается рост интереса к различным термодинамическим эффектам в пористых средах. Это связано с их многообразными практическими приложениями[4,5].

Особую важность упомянутые проблемы имеют в физике нефтегазоносных пластов. Поля давления в нефтегазоносных пластах в условиях разработки, как правило, нестационарны. Дросселирование нефти и газа приводит к проявлению баротермического эффекта – изменению температуры при течении нефти или газа в пористой среде в нестационарном поле давления. Величина барометрического эффекта в отличие от эффекта Джоуля – Томсона, наблюдающегося при стационарном дросселировании, зависит от коллекторских свойств пористой среды, времени, геометрии течения и других факторов. Эти особенности баротермического эффекта обеспечивают возможность его практического применения при исследовании скважин и пластов.

В основу исследований положена полная система уравнений для - той фазы (компонента), описывающих баротермический эффект. Ядром этой системы является уравнение для температуры с учетом термодинамических эффектов высокого порядка [9]

(I.2.1)

где первое слагаемое в левой части уравнения (I.2.1) описывает изменение температуры в пласте со временем, второе – за счет конвекции (перемещения больших объемов газа). Первое слагаемое в правой части ответственно за теплопроводность, второе – за межфракционный теплообмен, третье описывает адиабатический эффект, четвертое – эффект Джоуля-Томсона и пятое – влияние поля тяготения Земли.

Вторым уравнением системы является уравнение неразрывности , которое записывается в виде:

.

(I.2.2)

Фильтрация газа подчиняется закону Дарси

.

(I.2.3)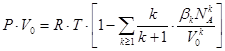