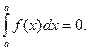Реферат: Интеграл и его свойства

Интегралы вида Для вычисления интеграла I₁ выделяется полный квадрат под знаком радикала:

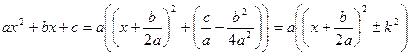
и применяется подстановка:

, dx=du.

В результате этот интеграл сводится к табличному:

В числителе интеграла I₂ выделяется дифференциал выражения, стоящего под знаком радикала, и этот интеграл представляется в виде суммы двух интегралов:

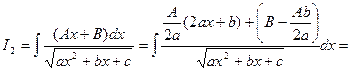
где I₁ – вычисленный выше интеграл.

Вычисление интеграла I₃ сводится к вычислению интеграла I₁ подстановкой:

Интеграл вида Частные случаи вычисления интегралов данного вида рассмотрены в предыдущем пункте. Существует несколько различных приемов их вычисления. Рассмотрим один из таких приемов, основанный на применении тригонометрических подстановок.

Квадратный трехчлен ax² + bx+ c путем выделения полного квадрата и замены переменной может быть представлен в виде Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:

Интеграл подстановкой

u=k sint (или u=k cost )

сводится к интегралу от рациональной функции относительно sintи cost.

Интегралы вида (m, n, p є Q , a, b є R ). Рассматриваемые интегралы, называемые интегралами от дифференциального бинома , выражаются через элементарные функции только в следующих трех случаях:

1) если p є Z , то применяется подстановка:

x= t^s ,

где s – общий знаменатель дробей mи n ;

2) если Z , то используется подстановка:

a+ bxⁿ = t^s ,

где s – знаменатель дроби

3) если Z , то применяется подстановка:

ax^-n +b=t^s ,

где s – знаменатель дроби

9. Понятие определенного интеграла, его геометрический смысл.

Определение. Если существует конечный передел интегральной суммы (8)

- (8)

при λ→0, не зависящий от способа разбиения τ _n отрезка [ a; b] на частичные отрезки и выбора промежуточных точек ξ _k , то этот предел называют определенным интегралом (или интегралом Римана) от функции f( x) на отрезке [ a; b] и обозначают:

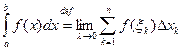
Если указанный предел существует, то функция f( x) называется интегрируемой на отрезке [a; b] (или интегрируемой по Риману ). При этом f( x) dx называется подынтегральным выражением, f( x) – подынтегральной функцией, х – переменной интегрирования, a и b – соответственно нижним и верхним пределами интегрирования.

Определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма, в случае, когда диаметр разбиения λ стремится к нулю.

Геометрический смысл определенного интеграла. Пусть функция y= f( x) непрерывна на отрезке [a; b] и f( x) ≥ 0 . Фигура, ограниченная графиком АВ функции y= f( x), прямыми x= a, x= b и осью Ох (рис. 1), называется криволинейной трапецией .

Интегральная сумма и ее слагаемые имеют простой геометрический смысл: произведение равно площади прямоугольника с основанием и высотой , а сумма представляет собой площадь заштрихованной ступенчатой фигуры (изображенной на рис. 1). Очевидно, что эта площадь зависит от разбиения τ _n отрезка [a; b] на частичные отрезки и выбора точек ξ _k .

Чем меньше , k=1, n, тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции. Следовательно, за точную площадь S криволинейной трапеции принимается предел интегральной суммы при λ→0 :

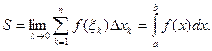
Таким образом, с геометрической точки зрения определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции.

10. Основные свойства определенного интеграла.

Рассмотрим свойства определенного интеграла.

1. Если нижний и верхний пределы интегрирования равны ( a= b), то интеграл равен нулю: