Реферат: Інтегральне числення
Замінимо задану криволiнiйну трапецію (рис. 2.1) ступінчатою фігурою, що складається з n прямокутників. Основи цих прямокутників однакові i дорівнюють 
, а висоти збігаються із значеннями
в початкових точках частинних iнтервалiв. Площа ступінчатої фігури i буде наближеним значенням визначеного інтеграла:
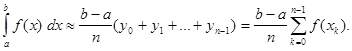(1)
Якщо висоти прямокутників є значення в кінцевих точках частинних iнтервалiв (рис. 2.2), то
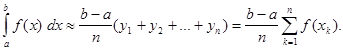(2)
Можна довести, що похибка наближеної формули зменшиться, якщо висотами прямокутників взяти значення функції в точках 
(середини відрізків 
, (рис. 2.3); тоді
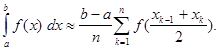(3)
Формули (1)-(3) називаються формулами прямокутників.
2. Формула трапецій . Замінимо криву f(х) не ступінчатою лiнiєю, як у попередньому випадку, а ламаною (рис. 2.3), сполучивши сусiднi точки (
). Тоді площа криволiнiйної трапеції наближено дорівнюватиме сумі площ прямокутних трапецій, обмежених вверху вiдрiзками цієї ламаної.
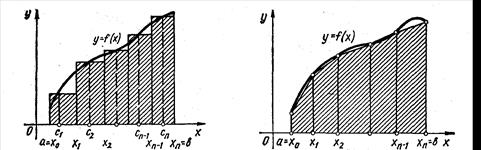
рис. 2.3 рис. 2.4
Площа k -ї трапеції дорівнює 
, де 
і 
—
основи трапеції, а 
- 
= - її висота. Тому
(4)
Формула (4) називається формулою трапецій.
3. Формула Сiмпсона . Під час виведення формули трапеції криву, яка є графіком функцій у = f (х), замінювали ламаною лiнiєю. Щоб дістати точніший результат, замінимо цю криву іншою кривою, наприклад параболою.
Покажемо спочатку, що через три рiзнi точки 
, які не лежать на одній прямій, можна провести лише одну параболу 
.
Справді, підставляючи в рівняння параболи координати заданих точок, дістанемо систему рівнянь:
(5)
визначник якої
,
оскільки числа 
за умовою рiзнi. Отже, ця система має єдиний розв’язок, тобто коефiцiєнти a , b i c параболивизначаються однозначно.
Зокрема, розв’язуючи систему (5) для точок А (-h ; 
), В (0; 
), С (h ; 
), дістанемо
рис. 2.5 рис. 2.6
Знайдемо площу S криволiнiйної трапеції, обмеженої параболою, яка проходить через точки А, В, С, і прямими х = -h, х = h,y =0 (рис. 2.5):
Розглянемо тепер криволiнiйну трапецію 
, обмежену кривою у = f (х) (рис. 2.6). Якщо через точки 
цієї кривої провести параболу , то за формулою (6)
(7)