Реферат: Інтегральне числення

= .

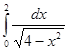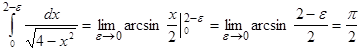Отже інтеграл збіжний.

Сформулюємо тепер ознаки збiжностi для невласних iнтегралiв другого роду.

Теорема 4. Якщо функції і неперервні на проміжку [ a ; b ), мають особливу точку х= b і задовольняють умову , то із збіжності інтеграла випливає збіжність інтеграла , із розбіжності інтеграла випливає розбіжність .

Приклад:

Дослідити на збіжність інтеграл : заданий інтеграл збігається, бо і збігається інтеграл .

Теорема 5. Нехай функції і на проміжку [ a ; b ) неперервні, додатні і мають особливість точці х= b , тоді якщо існує границя

,

то інтеграли і або одночасно збігаються, або одночасно розбігаються.

Приклад:

Дослідити на збіжність інтеграл : функціїf ( x )= та = мають особливість у точці х=0. Оскільки =, і інтеграл розбігається, то заданий інтеграл також розбігається.

Теорема 6. Якщо х= b – особлива точка функції і інтеграл збігається, то інтеграл також збігається.

Приклад: дослідити на збіжність інтеграл .

Заданий інтеграл збігається, тому що і збігається інтеграл .

4.Ефективність реклами . Логістична крива.

Розвиток багатьох процесів у економіці, в тому числі і на підприємствах, відображає логістична крива, яка характеризується часовою чи іншою залежністю параметрів об’єкта. Дану криву ще називають зигзагоподібною (S-подібною), оскільки вона нагадує букву S.