Реферат: Інтегральне числення
то заданий інтеграл збігається.
Слід зауважити, що із збіжності інтеграла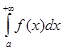 
не випливає, взагалі кажучи збіжність інтеграла 
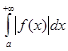. Ця обставина виправдовує такі означення.
Якщо разом з інтегралом 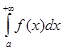збігається й інтеграл 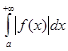, то інтеграл 
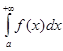називають абсолютно збіжним, а функцію 
- абсолютно інтегровною на проміжку 
.
Якщо інтеграл 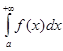збігається, а інтеграл 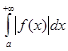розбігається, то інтеграл 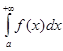називають умовно (або неабсолютно) збіжним.
Тепер теорему 3 можна перефразувати так: абсолютно збіжний інтеграл збігається.
Отже, для знакозмінної функції викладені тут міркування дають змогу встановити лише абсолютну збiжнiсть інтеграла. Якщо ж невласний інтеграл збігається умовно, то застосовують більш глибокі ознаки збiжностi.
2. Невласні інтеграли від необмежених функцій (невласні інтеграли другого роду).
Нехай функція визначена на проміжку 
. Точку х= b назвемо особливою точкою функції , якщо 
при 
(рис. 3.3)
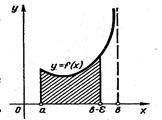
рис. 3.3
Нехай функція на відрізку 
при довільному 
, такому, що 
тоді існує скінченна границя
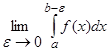, (20)
її називають невласним інтегралом другого роду і позначають так:
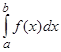(21)
Отже, за означенням
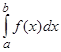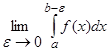= (22)
У цьому випадку кажуть, що інтеграл (21) існує або збігається. Якщо ж границя (20) нескінченна або не існує, то інтеграл (21) також називають невласним інтегралом, але розбіжним.
Аналогічно якщо х=а - особлива точка (рис. 3.4), невласний інтеграл визначається так:
=
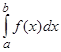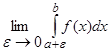
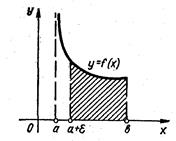
рис. 3.4
Якщо необмежена в околі якої-небудь внутрішньої точки 
, то за умови існування обох невласних інтегралів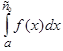 
і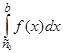 
за означенням покладають (рис. 3.5)
=+.
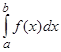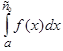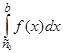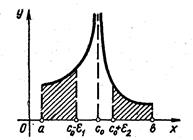
рис. 3.5
Нарешті, якщо а та b — особливі точки, то за умови існування обох невласних iнтегралiв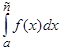 
і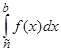 
за означенням покладають
=+,
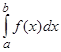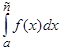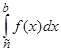де с - довільна точка інтервалу (a ; b ).
Приклад: