Реферат: Інтегральне числення

б)

Оскільки ця границя не існує, то інтеграл б) розбіжний.

У розглянутих прикладах обчислення невласного інтеграла ґрунтувалося на його означенні. Проте у деяких випадках немає необхiдностi обчислювати інтеграл, а достатньо знати, збіжний він чи ні.

Теорема 1. Якщо на проміжку функції f ( x ) і g ( x )неперервні і задовольняють умову , то із збіжності інтеграла

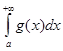(18)

випливає збіжність інтеграла

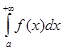, (19)

а із розбіжності інтеграла (19) випливає розбіжність інтеграла (18).

Наведена теорема має простий геометричний зміст (рис. 3.2); якщо площа більшої за розмірами необмеженої області є скiнченне число, то площа меншої області є також скiнченне число; якщо площа меншої області нескінченно велика величина, то площа більшої області є також нескінченно велика величина.

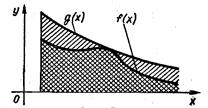
рис. 3.2

Приклад:

Дослідити на збіжність інтеграл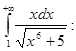

оскільки :

і інтеграл збігається, то за теоремою 1 заданий інтеграл також збігається.

Теорема 2. Якщо існує границя то інтеграли (18) і (19) або одночасно обидва збігаються, або одночасно розбігаються.

Ця ознака iнодi виявляється зручнішою, ніж теорема 1, бо не потребує перевірки нерiвностi .

Приклад:

Дослідити на збіжність інтеграл

оскільки інтеграл

збігається і ,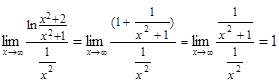

то заданий інтеграл також збігається.

В теоремах 1 і 2 розглядались невласні інтеграли від невід’ємних функцій. У випадку, коли пiдiнтегральна функція є знакозмінною, справедлива така теорема.

Теорема 3. Якщо інтеграл збігається, то збігається й інтеграл .

Приклад:

Дослідити на збіжність інтеграл :

тут підінтегральна функція знакозмінна; оскільки