Реферат: Інтегральне числення

Оскільки то залишковий член формули Сiмпсона

Таким чином, І= 1,089490,000012, тобто формула Сiмпсона значно точніша формули прямокутників і трапецій.

Невласні інтеграли. Ознаки збіжності невласних інтегралів

Раніше було введено визначений інтеграл як границю інтегральних сум, передбачаючи при цьому, що вiдрiзок інтегрування скiнченний, а пiдiнтегральна функція на цьому вiдрiзку обмежена. Якщо хоча б одна з цих умов порушується, то наведене вище означення визначеного інтеграла стає неприйнятним: у випадку нескінченного проміжку інтегрування його не можна розбити на п частинних вiдрiзкiв скiнченної довжини, а у випадку необмеженої функції інтегральна сума явно не має скiнченної границі. Узагальнюючи поняття визначеного інтеграла на ці випадки, приходимо до невласного інтеграла — інтеграла від функції на необмеженому проміжку або від необмеженої функції.

1. Невласні інтеграли з нескінченними межами інтегрування (невласні інтеграли першого роду).

Нехай функція f (х) визначена на проміжку [a ;) і інтегрована на будь-якому відрізку [a ;b ], де . Тоді, якщо існує скінченна границя

(13),

її називають невласним інтегралом першого роду і позначають так:

(14)

Таким чином, за означенням

(15)

У цьому випадку інтеграл (14) називають збіжним, а підінтегральну функцію f ( x ) – інтегрованою на проміжку (а; + ) .

Якщо ж границя (13) не існує або нескінченна, то інтеграл (14) називають також невласним але розбіжним, а функція f ( x ) – неінтегровною на [a ;).

Аналогічно інтегралу (15) означається невласний інтеграл на проміжку [; b ):

(16)

Невласний інтеграл з двома нескінченними межами визначається рівністю

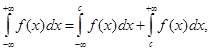(17)

де с – довільне число. Отже, інтеграл зліва у формулі (17) існує або є збіжним лише тоді, коли є збіжними обидва інтеграли справа. Можна довести, що інтеграл, визначений формулою (17), не залежить від вибору числа с.

З наведених означень видно, що невласний інтеграл не є границею інтегральних сум, а є границею означеного інтеграла із змінною межею інтегрування.

Зауважимо, що коли функція f (x ) неперервна і невід’ємна на проміжку [a ;) і коли інтеграл (16) збігається, то природно вважати, що він виражає площу необмеженої області (рис. 3.1)

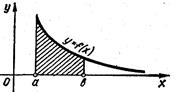
рис. 3.1

Приклад:

Обчислити невласний інтеграл або встановити його розбіжність

а) За формулою (15) маємо