Реферат: Использование дифференциальных уравнений в частных производных для моделирования реальных процес
СОДЕРЖАНИЕ
Введение………………………………………………………………………..……3
Глава 1. Уравнения гиперболического типа.
§1.1. Задачи, приводящие к уравнениям гиперболического типа..………………5
1.1.1. Уравнение колебаний струны..…………………………………………5
1.1.2. Уравнение электрических колебаний в проводах…….………………8
§1.2. Метод разделения переменных ……………………………………………..10
1.2.1. Уравнение свободных колебаний струны….…………………………10
Глава 2. Уравнения параболического типа.
§2.1. Задачи, приводящие к уравнениям параболического типа………………..17
2.1.1. Уравнение распространения тепла в стержне.……………………….17
2.1.2. Распространение тепла в пространстве.………………………………19
§2.2. Температурные волны.……………………………………………………….23
Глава 3. Моделирование с помощью дифференциальных уравнений в частных производных.
§3.1. Дифракция излучения на сферической частице……………………………29
Заключение………………………………………………………………………….40
Литература…………………………………………………………………………..41
ВВЕДЕНИЕ
Изучением дифференциальных уравнений в частных производных занимается математическая физика. Основы теории этих уравнений впервые были изложены в знаменитом «Интегральном исчислении» Л. Эйлера.
Классические уравнения математической физики являются линейными. Особенность линейных уравнений состоит в том, что если U и V – два решения, то функция aU + bV при любых постоянных a и b снова является решением. Это обстоятельство позволяет построить общее решение линейного дифференциального уравнения из фиксированного набора его элементарных решений и упрощает теорию этих уравнений.
Современная общая теория дифференциальных уравнений занимается главным образом линейными уравнениями и специальными классами нелинейных уравнений. Основным методом решения нелинейных дифференциальных уравнений в частных производных выступает численное интегрирование.
Круг вопросов математической физики тесно связан с изучением различных физических процессов. Сюда относятся явления, изучаемые в гидродинамике, теории упругости, электродинамике и т.д. Возникающие при этом математические задачи содержат много общих элементов и составляют предмет математической физики.
Постановка задач математической физики, будучи тесно связанной с изучением физических проблем, имеет свои специфические черты. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов.
Круг вопросов, относящихся к математической физике, чрезвычайно широк. В данной работе рассматриваются задачи математической физики, приводящие к уравнениям с частными производными.
Расположение материала соответствует основным типам уравнений. Изучение каждого типа уравнений начинается с простейших физических задач, приводящих к уравнениям рассматриваемого типа.
Глава 1. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
§1.1. Задачи, приводящие к уравнениям гиперболического типа.
Уравнения с частными производными 2-го порядка гиперболического типа наиболее часто встречаются в физических задачах, связанных с процессами колебаний. Простейшее уравнение гиперболического типа

называется волновым уравнением. К исследованию этого уравнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т.д.
1.1.1. Уравнение колебаний струны.
В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени, направлены по касательной к ее профилю. Пусть струна длины ![]() в начальный момент направлена по отрезку оси Оx от 0 до
в начальный момент направлена по отрезку оси Оx от 0 до ![]() . Предположим, что концы струны закреплены в точках
. Предположим, что концы струны закреплены в точках ![]() . Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя струны, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения – говорят, что струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.
. Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя струны, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения – говорят, что струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.
Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси Ox и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией ![]() , которая дает величину перемещения точки струны с абсциссой x в момент t.
, которая дает величину перемещения точки струны с абсциссой x в момент t.
 |
Рис. 1.1.
Так как мы рассматриваем малые отклонения струны в плоскости ![]() , то будем предполагать, что длина элемента струны
, то будем предполагать, что длина элемента струны ![]() равняется ее проекции на ось Ox, т.е.
равняется ее проекции на ось Ox, т.е. ![]() .1 Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.
.1 Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.
Рассмотрим элемент струны ![]() .
.
 | |
|
Рис. 1.2.
На концах этого элемента, по касательным к струне, действуют силы Т. Пусть касательные образуют с осью Ox углы ![]() . Тогда проекция на ось Ou сил, действующих на элемент
. Тогда проекция на ось Ou сил, действующих на элемент ![]() , будет равна
, будет равна ![]() . Так как угол
. Так как угол ![]() мал, то можно положить
мал, то можно положить ![]() , и мы будем иметь:
, и мы будем иметь:
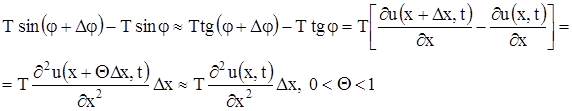
(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).
--> ЧИТАТЬ ПОЛНОСТЬЮ <--