Реферат: Использование дифференциальных уравнений в частных производных для моделирования реальных процес

Предполагается, что функции u (x, t) и m (t) ограничены всюду, т.е.

Запишем граничное условие в виде

(2’)

Из линейности уравнения теплопроводности следует, что действительная и мнимая части некоторого комплексного решения уравнения теплопроводности каждая в отдельности удовлетворяет тому же решению.

Если найдено решение уравнения теплопроводности, удовлетворяющее условию (2’), то его действительная часть удовлетворяет условию (2), а мнимая – условию

Итак, рассмотрим задачу:

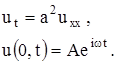(3)

Ее решение будем искать в виде

(4)

где и - неопределенные пока постоянные.

Подставляя выражение (4) в уравнение (3) и граничное условие, находим:

,

откуда

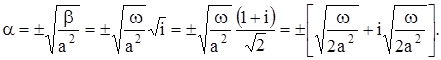
Для u (x, t) имеем:

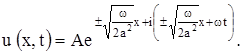(5)

Действительная часть этого решения

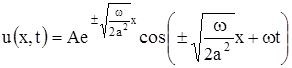(6)

удовлетворяет уравнению теплопроводности и граничному условию (2). Формула (6) в зависимости от выбора знака определяет не одну, а две функции. Однако только функция, соответствующая знаку минус, удовлетворяет требованию ограниченности. Таким образом, решение поставленной задачи получаем в виде

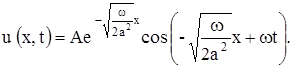(7)

На основании полученного решения можно дать следующую характеристику процесса распространения температурной волны в почве. Если температура поверхности длительное время периодически меняется, то в почве также устанавливаются колебания температуры с тем же периодом, причем:

1.Амплитуда колебаний экспоненционально убывает с глубиной

,

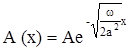т.е. если глубины растут в арифметической прогрессии, то амплитуды убывают в геометрической прогрессии (первый закон Фурье).

2. Температурные колебания в почве происходят со сдвигом фазы. Время запаздывания максимумов (минимумов) температуры в почве от соответствующих моментов на поверхности пропорционально глубине

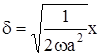
(второй закон Фурье).

3. Глубина проникновения тепла в почву зависит от периода колебаний температуры на поверхности. Относительное изменение температурной амплитуды равно

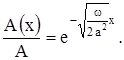
Эта формула показывает, что чем меньше период, тем меньше глубина проникновения температуры. Для температурных колебаний с периодами Т₁ и Т₂ глубины x₁ и x₂ , на которых происходит одинаковое относительное изменение температуры, связаны соотношением

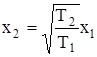
(третий закон Фурье). Так, например, сравнение суточных и годовых колебаний, для которых Т₂ = 365 Т₁ , показывает, что

т.е. что глубина проникновения годовых колебаний при одинаковой амплитуде на поверхности была бы в 19,1 раза больше глубины проникновения суточных колебаний.

Следует, однако, иметь в виду, что изложенная здесь теория относится к распространению тепла в сухой почве или горных породах. Наличие влаги усложняет температурные явления в почве, при замерзании происходит выделение скрытой теплоты, не учитываемое этой теорией.

Температуропроводность является одной из характеристик тела, важных для изучения его физических свойств, а также для различных технических расчетов. На