Реферат: Использование дифференциальных уравнений в частных производных для моделирования реальных процес

Рассмотрим элементарный объем υ. Пусть за время t его температура поднялась на u. Очевидно, что количество тепла, затраченное на это повышение температуры элемента υ, будет равно

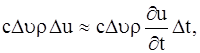
где с – теплоемкость вещества, ρ – плотность. Общее количество тепла, затраченное на повышение температуры в объеме V за время t, будет

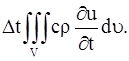
Но это есть тепло, поступающее в объем V за время t; оно определено формулой (11) . Таким образом, имеет место равенство

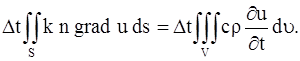
Сокращая на t, получаем:

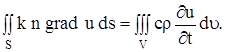(12)

Поверхностный интеграл, стоящий в левой части этого равенства, преобразуем по формуле Остроградского (в векторной форме, где F – дивергенция векторного поля, – замкнутая поверхность)

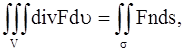
полагая F = k grad u:

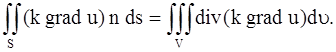
Заменяя двойной интеграл, стоящий в левой части равенства (12), тройным интегралом, получим:

(13)

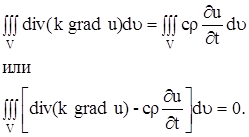
Применив теорему о среднем к тройному интегралу, стоящего слева, получим :

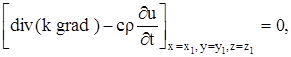(14)

где P (x, y, z) – некоторая точка объема V.

Так как мы можем выделить произвольный объем V в трехмерном пространстве, где происходит распространение тепла, и так как мы предполагаем, что подынтегральная функция в равенстве (13) непрерывна, то равенство (14) будет выполняться в каждой точке пространства. Итак,

(15)

Но

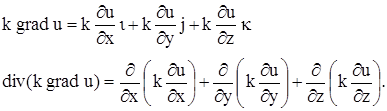
Подставляя в уравнение (15), получаем:

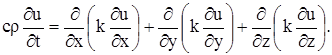(16)

Если k – постоянное, то

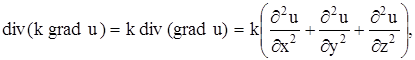
и уравнение (15) в этом случае дает:

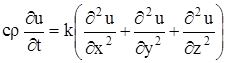
или, положив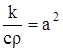

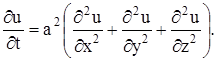(17)

Коротко уравнение (17) записывается так:

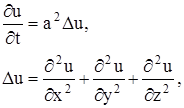
где u – оператор Лапласа. Уравнение (17) и есть уравнение теплопроводности в пространстве. Для того чтобы найти единственное решение, отвечающее поставленной задаче, нужно задать краевые условия.

Пусть имеем тело , поверхность которого . В этом теле рассматривается процесс распространения тепла. В начальный момент температура тела задана. Это соответствует тому, что известно значение решения при t = 0 – начальное условие:

u (x, y, z, 0) = φ (x, y, z). (18)

Кроме того, должна быть известна температура в любой точке М поверхности тела в любой момент времени t – граничное условие:

u (М, t) = ψ (М, t). (19)

(Возможны и другие граничные условия.)

Если искомая функция u (x, y, z, t) не зависит от z, что соответствует тому, что температура не зависит от z, то получаем уравнение:

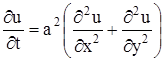(20)

- уравнение распространения тепла на плоскости. Если рассматривается распространения тепла в плоской области D с границей С, то граничные условия, аналогично (18) и (19), формулируются так:

u (x, y, 0) = φ (x, y),

u (М, t) = ψ (М, t),

где φ и ψ – заданные функции, М – точка границы С.

Если же функция u не зависит ни от z, ни от y, то получаем уравнение

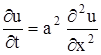
- уравнение распространения тепла в стержне.

§2.2. Температурные волны.

Задача о распространении температурных волн в почве является одним из первых примеров приложения математической теории теплопроводности, развитой Фурье, к изучению явлений природы.

Температура на поверхности земли носит, как известно, ярко выраженную суточную и годовую периодичность. Обратимся к задаче о распространении периодических температурных колебаний в почве, которую будем рассматривать как однородное полупространство . Эта задача является характерной задачей без начальных условий, так как при многократном повторении температурного хода на поверхности влияние начальной температуры будет меньше влияния других факторов, которыми мы пренебрегаем (например, неоднородность почвы). Таким образом, приходим к следующей задаче:

найти ограниченное решение уравнения теплопроводности

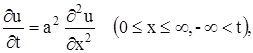(1)