также удовлетворяет этому уравнению и граничным условиям (9). Начальные условия позволяют определить A_n и B_n . Потребуем, чтобы функция (24) удовлетворяла условиям (10)

(25)

Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция f(x), заданная в промежутке , разлагается в ряд Фурье

(26)

где

(27)

Если функции j(x) и y(x) удовлетворяют условиям разложения в ряд Фурье, то

(28)

(29)

Сравнение этих рядов с формулами (25) показывает, что для выполнения начальных условий надо положить

(30)

чем полностью определяется функция (24), дающая решение исследуемой задачи.

Итак, мы доказали, что ряд (24), где коэффициенты A_n и B_n определены по формуле (30), если он допускает двукратное почленное дифференцирование, представляет функцию u (x, t), которая является решением уравнения (1) и удовлетворяет граничным и начальным условиям (9) и (10).

Замечание. Решая рассмотренную задачу для волнового уравнения другим методом, можно доказать, что ряд (24) представляет решение и в том случае, когда он не допускает почленного дифференцирования. При этом функция должна быть дважды дифференцируемой, а - один раз дифференцируемой.

Глава 2. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА

§2.1. Задачи, приводящие к уравнениям гиперболического типа.

2.1.1. Уравнение распространения тепла в стержне.

Рассмотрим однородный стержень длины . Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.

Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, а другой – с точкой х = .

Рис. 2.1.

Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой

(1)

где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.

Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х₁ и х₂ (х₂ – х₁ = х). Количество тепла, прошедшего через сечение с абсциссой х₁ за время t, будет равно

(2)

то же самое с абсциссой х₂ :

(3)

Приток Q₁ - Q₂ в элемент стержня за время t будет равняться:

(4)

Этот приток тепла за время t затратился на повышение температуры элемента стержня на величину u:

или

(5)

где с – теплоемкость вещества стержня, – плотность вещества стержня (xS – масса элемента стержня).

Приравнивая выражения (4) и (5) одного и того же количества тепла , получим:

(6)

Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.

Чтобы решение уравнения (6) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (6) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для , следующие:

u (x, 0) = φ(x), (7)

u (0, t) = ψ₁ (t), (8)

u (, t) = ψ₂ (t). (9)

Физическое условие (7) (начальное условие) соответствует тому, что при в разных сечениях стержня задана температура, равная φ(x). Условия (8) и (9) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х = поддерживается температура, равная ψ₁ (t) и ψ₂ (t) соответственно.

Доказывается, что уравнение (6) имеет единственное решение в области , удовлетворяющее условиям (7) – (9).

2.1.2. Распространение тепла в пространстве.

Рассмотрим процесс распространения тепла в трехмерном пространстве. Пусть u (x, y, z, t) – температура в точке с координатами (x, y, z) с момент времени t. Опытным путем установлено, что скорость прохождения тепла через площадку s, т. е. количество тепла, протекающего за единицу времени, определяется формулой (аналогично формуле (1))

(10)

где k – коэффициент теплопроводности рассматриваемой среды, которую мы считаем однородной и изотропной, n – единичный вектор, направленный по нормали к площадке s в направлении движения тепла. Таким образом, можем записать:

где – направляющие косинусы вектора n, или

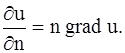
Подставляя выражение в формулу (10), получаем:

Q = -k n grad u s.

Количество тепла, протекающего за время ∆t через площадку ∆s, будет равно:

Qt = -k n grad u t s.

Вернемся к поставленной задаче. В рассматриваемой среде выделим малый объем V, ограниченный поверхностью S. Количество тепла, протекающего через поверхность S, будет равно:

(11)