Реферат: Использование дифференциальных уравнений в частных производных для моделирования реальных процес

где – постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.

Из соотношения (14) получаем обыкновенные дифференциальные уравнения для определения функций X (x) и T (t)

(15)

(16)

Граничные условия (11) дают:

Отсюда следует, что функция X (x) должна удовлетворять дополнительным условиям:

X(0) = X() = 0, (17)

Так как иначе мы имели бы

в то время как задача состоит в нахождении нетривиального решения. Для функции T (t) в основной вспомогательной задаче никаких дополнительных условий нет.

Таким образом, в связи с нахождением функции X (x) мы приходим к простейшей задаче о собственных значениях:

найти те значения параметра 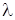, при которых существуют нетривиальные решения задачи:

(18)

а также найти эти решения. Такие значения параметра называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (18). Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.

Рассмотрим отдельно случаи, когда параметр отрицателен, равен нулю или положителен.

1. При ‹ 0 задача не имеет нетривиальных решений. Действительно, общее решение уравнения (15) имеет вид

Граничные условия дают:

Х (0) = С₁ + С₂ = 0;

т. е.

Но в рассматриваемом случае – действительно и положительно, так что . Поэтому

С₁ =0, С₂ = 0

и, следовательно,

Х (х)0.

2. При = 0 также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид

Х (х) = С₁ х + С₂ .

Граничные условия дают:

т. е. С₁ = 0 и С₂ = 0 и, следовательно,

Х (х)0.

3. При › 0 общее решение уравнения может быть записано в виде

Граничные условия дают:

Если Х(х) не равно тождественно нулю, то D₂ 0, поэтому

(19)

или

где n- любое целое число. Следовательно, нетривиальные решения задачи (18) возможны лишь при значениях

Этим собственным значениям соответствуют собственные функции

где D_n – произвольная постоянная.

Итак, только при значениях , равных

(20)

существуют нетривиальные решения задачи (11)

(21)

определяемые с точностью до произвольного множителя, который мы положили равным единице. Этим же значениям _n соответствуют решения уравнения (9)

(22)

где A_n и B_n – произвольные постоянные.

Возвращаясь к задаче (1), (9), (10), заключаем, что функции

(23)

являются частными решениями уравнения (1), удовлетворяющими граничным условиям (11) и представимыми в виде произведения (12) двух функций, одна из которых зависит только от х, другая – от t. Эти решения могут удовлетворить начальным условиям (10) нашей исходной задачи только для частных случаев начальных функций j(x) и y(x).