Реферат: Изучение основ комбинаторики и теории вероятностей

Комбинаторика, пройдя многовековой путь развития, обретя собственные методы исследования, с одной стороны, широко используется при решении задач алгебры, геометрии, анализа, с другой стороны, сама использует геометрические, аналитические и алгебраические методы исследования. В конце XVIII века учёные, принадлежащие комбинаторной школе Гинденбурга, попытались построить общую комбинаторную теорию, используя бесконечные ряды. Исследователи этой школы изучили большое количество преобразований рядов: умножение, деление, возведение в степень, извлечение корней, обращение рядов, разложение трансцендентных функций. Использование производящих функций в комбинаторике можно отнести к (уже) классическим традициям.

1.2. Предмет комбинаторики

Комбинаторный анализ, комбинаторная математика, комбинаторика, - раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией. Поэтому можно сказать, что целью комбинаторного анализа является изучение комбинаторных конфигураций, в частности, вопросы их существования, алгоритмы построения, решение задач на перечисление. Примерами комбинаторных конфигураций являются перестановки, размещения и сочетания; блок-схемы и латинские квадраты.

В Математическом Энциклопедическом Словаре говорится, что комбинаторика- один из разделов дискретной математики, который приобрел важное значение в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной технике, кибернетике.

В Большой Советской Энциклопедии говорится, что комбинаторика - это раздел математики в котором изучаются некоторые операции над конечными множествами.

1.3. Основные понятия и теоремы комбинаторики

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.

1.3.1. Основные правила комбинаторики

При вычислении количества различных комбинаций используются правила сложения и умножения. Сложение используется, когда множе­ства не совместны. Умножение - когда для каждой комбинации перво­го множества имеются все комбинации (или одинаковое число комби­наций) второго множества.

Пример. Из 28 костей домино берутся 2 кости. В каком числе комбинаций вторая кость будет приложима к первой?

На первом шаге имеется два варианта: выбрать дубль (7 комбина­ций) или недубль (21 комбинация). В первом случае имеется 6 вариан­тов продолжения, во втором - 12.

Общее число благоприятных комбинаций равно: .

А всего вариантов выбора 2 костей из 28 равно 378; т. е. при боль­шом числе экспериментов в 7 случаях из 9 (294/378 = 7/9) при выборе 2 костей одна кость окажется приложимой к другой.

1.3.2. Размещения с повторениями

Размещение с повторением также в комбинаторике называется кортежем.

Рассмотрим задачу: сколько разных числовых последовательностей, длины 5, можно со­ставить из 10 цифр?

Перенумеруем разряды:

1

2

3

4

5

В первый разряд можно поставить одну из 10 цифр. Независимо от того, какая цифра поставлена, во второй разряд можно также поставить одну из 10 цифр и т. д. Всего получается 10⁵ различных чисел.

Для двоичной системы счисления (используются только две цифры: 0 или 1) получаем 2⁵ различных числовых последовательностей. Для системы с основанием к и числом разрядов п соответственно получаем:

(1)

n -число позиций (разрядов); k -число элементов в каждой позиции (цифр).

В общем виде задача ставится следующим образом: имеется k ти­пов предметов (количество предметов каждого типа неограниченно) и п позиций (ящиков, кучек, разрядов). Требуется определить, сколько раз­ных комбинаций можно составить, если в позициях предметы могут повторяться? Ответ дается формулой (1).

Пример. Сколько разных числовых последовательностей может содержать 10-разрядное слово в троичной системе счисления? В первый разряд можно поста­вить один из трех символов (0, 1 или 2), во второй разряд - также один из трех символов и т. д. Всего получаем З¹⁰ чисел.

В некоторых случаях имеются ограничения на количество разных предметов, которые можно помещать на позиции. Пусть, например, имеется п позиций и на каждую i -ю позицию можно поставить k _i пред­метов. Сколько в этом случае существует разных расстановок предме­тов по позициям?

Легко обосновывается формула:

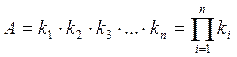(2)

Пример. В эстафете 100+200+400+800 метров на первую пози­цию тренер может выставить одного из 3 бегунов, на вторую - одного из 5, на третью - одного из 6, на четвертую - единственного бегуна (на каждую позицию выставляются разные бегуны). Сколько вариантов рас­становки участников эстафетного забега может составить тренер?

В соответствии с формулой (2) получаем, что число вариантов рав­но: .