Реферат: Изучение основ комбинаторики и теории вероятностей

1.4. Основные комбинаторные задачи

1.4.1. Главная теорема комбинаторики (Теорема о включениях и исключениях)

Пример. На предприятии работает 67 человек. Из них 48 знают английский, 35 - немецкий и 27 - оба языка. Сколько человек не знают ни английского, ни немецкого?

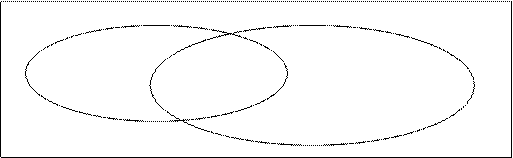
Результат можно получить следующим образом. Построим диаграм­му, на которой изобразим прямоугольник, соответствующий общему числу работающих (67) и две пересекающиеся области А и В по 48 и 35 человек (знающих английский и немецкий языки). На диаграмме об­щая часть этих двух областей соответствует 27 - количеству работаю­щих, которые знают оба языка. Требуется найти область прямоугольни­ка, не входящую ни в область А, ни в область В.

67

A=48 AB=27 B=35

Очевидно, что N = 67 - 48 - 35 + 27 = 11.

Главная теорема комбинаторики (Теорема о включениях и ис­ключениях)

Пусть имеется множество из N объектов произвольной природы. На этом множестве пусть задано п свойств. Каждый объект может обла­дать либо не обладать некоторыми из этих свойств. Сами свойства обо­значим:. Будем обозначать N() - количество объек­тов точно обладающих свойством и может быть какими-то другими, а N () - число объектов не обладающих ни свойством , ни свойством . Тогда число объектов, не обладающих ни одним из пере­численных свойств:

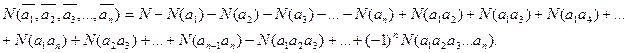
(8)

Продолжение примера. Пусть теперь 20 человек знают французс­кий, 12 - английский и французский, 11 - английский и немецкий и 5 - все три языка.

Тогда в соответствии с теоремой количество человек, не знающих ни одного из трех перечисленных языков (но может быть знающих ки­тайский язык), равно N = 67 - 48 - 35 - 20 + 27 +12+11-5 = 9.

Решето Эратосфена

Выпишем все числа от 1 до N. Сколько чисел делится на k ?Очевид­но, [N / k ],где [х ] обозначает целую часть числа х. Тогда, легко подсчи­тать количество чисел, не делящихся в данном диапазоне на k ₁ k ₂ , k ₃ ...

Пример. Сколько чисел от 1до 100 не делятся ни на 5, ни на 7?

Воспользуемся теоремой о включениях и исключениях. Под первым свойством чисел будем понимать делимость на 5, под вторым – делимость на 7. На 5 делятся 20 чисел. На 7 делятся 14 чисел. На 35 делятся 2 числа. Следовательно, не делятся на 5 и 7: 100 - 20 - 14 + 2 = 68 чисел.

1.4.2. Частный случай теоремы о включениях и исключениях

В некоторых случаях количество объектов, обладающих определен­ным набором свойств, зависит только от числа этих свойств. Тогда фор­мула для подсчета числа объектов, не обладающих ни одним из выде­ленных свойств, упрощается.

При произвольном п имеем:

В последнем примере предыдущего параграфа мы использовали этот частный случай главной теоремы комбинаторики. В общем случае при перестановке п предметов количество расстановок, при которых ни один предмет не находится на своем месте:

(9)

Полученное значение D_n иногда называют формулой полного беспо­рядка или субфакториалом. Субфакториал D_n можно представить и так:

.

где выражение в [...] стремится к е ^-1 при неограниченном возраста­нии.

Субфакториал имеет свойства, похожие на свойства обычного фак­ториала. Например,

- для обычного факториала,

- для субфакториала.