Реферат: Изучение основ комбинаторики и теории вероятностей

Сочетаниями называют комбинации, составленные из n различных элементов по k элементов, которые отличаются хотя бы одним элементом.

Формула (6) может быть получена следующим образом. Выберем по очереди к предметов из п. Число вариантов будет равно 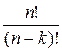. В этих расстановках к выбранных предмета имеют свои определенные позиции. Однако нас не интересуют в данном случае позиции выбран­ных предметов. От перестановки этих предметов интересующий нас вы­бор не меняется. Поэтому полученное выражение нужно разделить на

Пример 1. Из группы в 25 человек нужно выбрать троих для рабо­ты в колхозе. Если выбирать их последовательно, сначала первого, по­том второго, потом третьего, то получим варианта. Но так как нас не интересует порядок выбора, а только состав выбранной бри­гады, поэтому полученный результат нужно разделить еще на 3!

Пример 2. В середине 60-х годов в России появились две лоте­реи, которые были названы "Спортлото": лотерея 5/36 и 6/49. Рассмотрим одну из них, например, 6/49. Играющий покупает билет, на котором имеется 49 клеточек. Каждая клеточка соответ­ствует какому-либо виду спорта. Нужно выделить (зачеркнуть) 6 из этих клеточек и отправить организаторам лотереи. После розыгрыша лоте­реи объявляются шесть выигравших номеров. Награждается угадав­ший все шесть номеров, пять номеров, четыре номера и даже угадав­ший три номера. Соответственно, чем меньше угадано номеров (видов спорта), тем меньше выигрыш.

Подсчитаем, сколько существует разных способов заполнения кар­точек "Спортлото" при условии, что используется лотерея 6/49. Ка­залось бы, заполняя последовательно номер за номером, получим: . Но ведь порядок заполнения не имеет значения, тогда получаем:

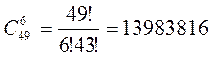
Эту же задачу можно решить и другим способом. Выпишем все но­мера подряд и под выбираемыми номерами поставим 1, а под осталь­ными - 0. Тогда различные варианты заполнения карточек будут отли­чаться перестановками. При этом переставляются 6 предметов одного вида (единицы) и 49 - 6 = 43 предмета другого вида (нули), т. е. опять

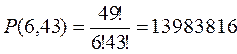
Если все участники заполняют карточки по-разному, то в среднем один из примерно 14 миллионов угадает все 6 номеров. А сколько чело­век в среднем угадают 5 номеров?

Выберем один из угаданных номеров () и заменим его на один

из не угаданных (). Итого: человек из 14 миллионов

угадают 5 номеров. А сколько угадают 4 номера? Выберем из 6 уга­данных два и затем из 43 не угаданных тоже два и перемножим число вариантов выбора. Тогда получим:человек.

Аналогично найдем, что 3 номера угадают 246820 человек, т. е. при­мерно 1,77% от всех играющих.

1.3.7. Сочетания с повторениями

Пример. Требуется купить 7 пирожных. В магазине имеются пирожные следующих видов: эклеры, песочные, слоеные и наполеоны. Сколько вариантов выбора? Решение: выбранные пирожные заменяем единицами, и добавляем три нуля (разделителя). Каждой перестановке однозначно соответствует некоторый выбор. Например, одному из ва­риантов покупки будет соответствовать такой код: 1101110101 . Пиро­жные покупаются следующим образом. Количество единиц слева до первого нуля соответствует покупке эклеров, между первым и вторым нулем - покупке песочных, между вторым и третьим - покупке слое­ных, единицы после третьего нуля соответствуют числу покупаемых наполеонов. В случае приведенного кода покупается 2 эклера, 3 песоч­ных, 1 слоеное и 1 наполеон. Количество вариантов покупки пирожных равно числу перестановок из 7 объектов одного типа (единиц) и 3 объек­тов второго типа (нулей).

Пусть имеются предметы п разных типов (без ограничения числа предметов каждого типа) и требуется определить, сколько комбинаций можно сделать из них, чтобы в каждую комбинацию входило к предме­тов. Каждую комбинацию шифруем с помощью 0 и 1, причем 1 соот­ветствуют предметам, а 0 выполняют функцию разделителей. Тогда записав к единиц и добавив п - 1 нуль, мы получим комбинацию, при которой выбираются к предметов первого типа и ни одного предмета остальных типов. Переставляя всеми способами эти к единиц и п - 1 нуль, мы будем каждый раз получать некоторую расстановку, состоя­щую из к предметов. Тогда

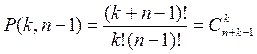(7)

1.3.8. Свойства чисел сочетаний

Приведем некоторые свойства чисел сочетаний, которые часто ис­пользуются при преобразованиях формул комбинаторики.

1. .

2. .

3. .

Первое свойство совершенно очевидно. Давайте проверим:

.

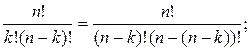
Второе легко доказывается, если оба члена правой части представить по формуле (6).

Третье свой­ство можно доказать методом математической индукции. Для приме­ра, при п = 2 имеем:

.

Для п = 3 получаем:

.

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством