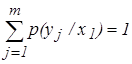то всегда можно найти такой способ кодирования, который обеспечит передачу всех сообщений источника, причем скорость передачи информации будет весьма близкой к пропускной способности канала.

Теорема не отвечает на вопрос, каким образом осуществлять кодирование.

Пример 1. Источник вырабатывает 3 сообщения с вероятностями:

p ₁ = 0,1; p ₂ = 0,2 и p ₃ = 0,7.

Сообщения независимы и передаются равномерным двоичным кодом (m = 2 ) с длительностью символов, равной 1 мс. Определить скорость передачи информации по каналу связи без помех.

Решение: Энтропия источника равна

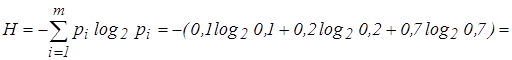
[бит/с].

Для передачи 3 сообщений равномерным кодом необходимо два разряда, при этом длительность кодовой комбинации равна 2t.

Средняя скорость передачи сигнала

V =1/2 t = 500 [1/ c ].

Скорость передачи информации

C = vH = 500 × 1,16 = 580 [бит/с].

2.2 Дискретный канал связи с помехами

Мы будем рассматривать дискретные каналы связи без памяти.

Каналом без памяти называется канал, в котором на каждый передаваемый символ сигнала, помехи воздействуют, не зависимо от того, какие сигналы передавались ранее. То есть помехи не создают дополнительные коррелятивные связи между символами. Название «без памяти» означает, что при очередной передаче канал как бы не помнит результатов предыдущих передач.

При наличии помехи среднее количество информации в принятом символе сообщении – Y , относительно переданного – X равно:

.

Для символа сообщения X_T длительностиT , состоящегоиз n элементарных символов среднее количество информации в принятом символе сообщении – Y_T относительно переданного – X_T равно:

I(Y_T , X_T ) = H(X_T ) – H(X_T /Y_T ) = H(Y_T ) – H(Y_T /X_T ) = n [H(Y) – H (Y/X). (9)

Для определения потерь в дискретном канале связи используется канальная матрица (матрица переходных вероятностей), позволяющая определить условную энтропию характеризующую потерю информации на символ сообщения.

Скорость передачи информации по дискретному каналу с помехами

равна:

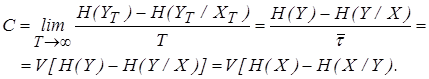(10)

Пропускная способность дискретного канала при наличии помех равна максимально допустимой скорости передачи информации, причем максимум разыскивается по всем распределениям вероятностей p ( x ) на X и, поскольку, энтропия максимальна для равномерного распределения (для равновероятных символов сообщения), то выражение для пропускной способности имеет вид:

. (11)

Как видно из формулы, наличие помех уменьшает пропускную способность канала связи.

Пример. По каналу связи передаются сообщения, вероятности которых соответственно равны:

p ( x ₁ )=0,1; p ( x ₂ )=0,2; p ( x ₃ )=0,3; p ( x ₄ )=0,4.

Канальная матрица, определяющая потери информации в канале связи имеет вид: