Реферат: Компьютерные технологии решения оптимизационных задач управления
4. Построение и оформление диаграмм
5. Вставка более 200 функций
6. Обмен данными
7. Обработка списков
8. Анализ данных
9. Конфигурирование программы MS Excel
10. Встроенный язык VBA
11. Решение задач оптимизации с использованием надстройки Поиск решения
Система REDUCE
Данная система хронологически сможет считаться одной из старейших систем компьютерной алгебры, её первая версия появилась в 1969 г. Входной язык по характеру аналогичен языкам программирования. Для решения задачи требуется составить программу, которая состоит из серии команд, представляющих собой вызовы функций, условные операторы, циклы и т. п. Система при переходе к каждому следующему этапу интерпретирует команду в порядке поступления и выполняет её.
Система REDUCE рассчитана на профессиональное использование при сложных вычислениях, имеет большую библиотеку функций и реализуется на “больших” ЭВМ, что делает её применение в образовании практически невозможным.
Система Macsyma.
Система Macsyma, как и REDUCE, структурирована по образцу высокоуровневых языков программирования. Её новая версия (Macsyma 2.3) обладает рядом интересных особенностей, к которым можно отнести применение самых современных алгоритмов численных расчётов библиотек, таких как LINPACK и EISPACK, благодаря встроенным в систему командам программы MatLab. Кроме того, имеется встроенная электронная таблица для обработки данных и специальное мощное, взаимосвязанное с интерфейсом Macsyma, дополнение, предназначенное для решения дифференциальных уравнений с частными производными методом конечных элементов. Как и REDUCE, данная система рассчитана на использование математиками-профессионалами.
Система Derive
Система Derive, на взгляд многих пользователей, очень органично сочетает возможности проведения численных и символьных вычислений с простотой в обращении и невысокими требованиями к используемой компьютерной технике. Последнее обстоятельство является особенно существенным аргументом в пользу применения данной системы в образовании. Derive имеет многооконный интерфейс пользователя и удобную систему меню. Языком реализации является “Lisp” — один из самых известных функциональных языков, ориентированный на решение задач искусственного интеллекта и построение экспертных систем. Ввод математических символов выполняется с клавиатуры набором слов, которые порождают на мониторе изображения соответствующих математических символов, при необходимости — в двумерном виде (как, например, обыкновенные дроби). Встроенный графический редактор позволяет получать двумерные графики в декартовых и полярных системах координат и трёхмерные графики, с возможностью автоматического масштабирования.
Существенным достоинством современных версий Derive является то, что они относятся к расширяемым системам, способным адаптироваться к решению конкретных задач, формулируемых данным пользователем.
Однако недостатком системы Derive является ограниченная возможность для программирования пользователем. Использование системы Derive в образовании возможно, и это сегодня уже реализуется в некоторых вузах и даже школах.
3.Понятие о численных методах лежащих в основе компьютерной реализации процесса принятия оптимизационных решений
Разнообразие нелинейных задач математического программирования (с полной или неполной информацией) вызывает необходимость разработки методов оптимизации, не связанных непосредственно с анализом условий существования X* и целиком базирующихся на вычислительных и логических операциях.
Идеи этих методов обычно просты; как правило, они следуют из эвристических соображений, сводя проблему решения задачи к построению надлежащего алгоритма поиска X*, г*, причем желаемые свойства таких алгоритмов оговариваются заранее.
Численные методы играют значительную роль в решении важных для практики оптимизационных решений.
В отдельных случаях бывает трудно определить, к какому классу относится та или иная задача и существует ли для нее обоснованный метод решения.
На выбор метода может влиять стремление максимально использовать мощности ЭВМ с целью снижения затрат на исследования (если подобная перспектива реальна).
Указанные обстоятельства позволяют рассматривать численные методы оптимизации как необходимое средство решения проблем поиска оптимума в исследованиях, различных по содержанию и сложности.
Рассмотренные положения позволяют обосновать приемлемость тех или иных численных методов для решения экстремальных задач.
Вычисление определенных интегралов.
Рассмотрим пример: ![]() .
.
В первую очередь необходимо создать функцию,вычисляющую подынтегральное выражение.
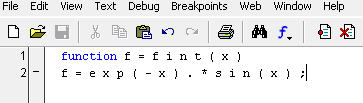
Для вычисления интеграла вызовем функцию quad, задав первым аргументом ссылку на функцию fint, а вторым и третьим — нижний и верхний пределы интегрирования.
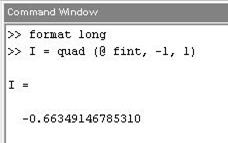
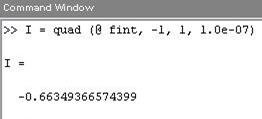
По умолчанию функция quad вычисляет приближенное значение интеграла с точностью 10-6. Для изменения точности вычислений следует задать дополнительный четвертый аргумент:
Вычисление двойных интегралов.
В MATLAB определена функция dblquad для приближенного вычисления двойных интегралов. Как и в случае вычисления определенных интегралов, следует написать файл-функцию для вычисления подынтегрального выражения. Вычислим интеграл:
![]()
Следовательно, функция должна содержать два аргумента x и y:
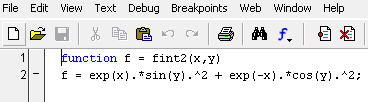
Функция dblquad имеет пять входных аргументов. При ее вызове необходимо учесть, что первыми задаются пределы внутреннего интеграла по х, а вторыми — внешнего по у: