Реферат: Компьютерные технологии решения оптимизационных задач управления

3. точка называется локальным минимумом, если для

4. точка называется строгим локальным минимумом, если для

Следствие: любая точка глобального минимума является локальным минимумом, обратное не верно.

Аналитический способ нахождения локального минимума.

- дифференцируема

- необходимое условие точки локального минимума.

Численные методы

Пусть функция задана на интервале , при этом существует такая точка , что на – монотонно убывает, а на – монотонно возрастает, то функция унимодальная.

а b

Если из того что следует, что , то функция называется монотонно возрастающей. Если из того что следует, что , то функция называется монотонно убывающей.

Методы одномерного поиска

Разобьем и вычислим значение функции в каждой точке.

искомый минимум

В результате остается интервал меньшего размера, к которому применяется тот же метод, и находим еще один интервал, в конце находим интервал с заведомо нужной точкой.

Интервал неопределенности – интервал, в котором заведомо находится точка минимума. Наиболее эффективное разбиение – двумя точками на 3 равных отрезка.

1)

2)

- после выполнения n шагов сокращение исходного интервала

- точность с которой надо найти решение задачи.

N=2n, где n – число шагов, N – число вычислений (мера эффективности данного решения).

Метод золотого сечения

Точки должны быть расположены на равном расстоянии.

а b

; ; ;

; - золотое сечение.

а

- величина сокращения на каждом шаге

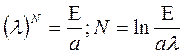
число итераций растет как логарифм функции.

Одномерная оптимизация с использованием производных

. Пусть целевая функция дифференцируема .

точка локального минимума	точка локального максимума	точка перегиба

Методы для нахождения корня уравнения функции 1-ой производной от исходной

Нахождение локального минимума или максимума сводится к нахождению корней первой производной от данной

f ’( x )=0

Если f’(x) представляет собой многочлен, то уравнение называется алгебраическим (полиномиальным), если f’(x) представлена тригонометрическими, логарифмическими, показательными и т.п. функциями, то уравнение называется трансцендентным .( вдальнйшем вместо f ’( x ) будем употреблять f ( x ) )

Решение уравнения вида разбивается на два этапа:

1. отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;

2. вычисление выделенного корня с заданной точностью.