Реферат: Компьютерные технологии решения оптимизационных задач управления

Интегралы, зависящие от параметра.

Функции quad и quadl позволяют находить значения интегралов, зависящих от параметров. Аргументами функции, вычисляющей подынтегральное выражение, должна быть не только переменная интегрирования, но и все параметры. Значения параметров указываются через запятую, начиная с шестого аргумента quad или quadl.

Решим интеграл:

Зададим функцию

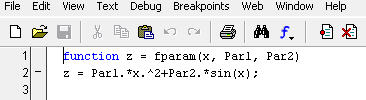
Используя quad, вычислим интеграл:

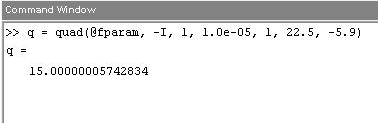
4.Идеи методов одномерной оптимизации

Численные методы оптимизации классифицируются следующим образом.

1. По размерности решаемых задач: одномерные; многомерные.

Одномерная оптимизация: Метод сканирования. Метод деления пополам. Метод золотого сечения. Метод параболической аппроксимации.

Многомерная безусловная градиентная оптимизация: Метод градиента. Метод наискорейшего спуска. Метод сопряженных градиентов. Метод тяжелого шарика.

Многомерная безградиентная оптимизация: Метод Гаусса-Зайделя (покоординатный спуск). Метод Розенброка. Симплексный метод (метод дифференцируемого многогранника). Метод параллельных касательных.

Многомерная случайная оптимизация: Метод слепого поиска. Метод случайного направления. Метод поиска с «наказанной случайностью». Метод с «блуждающим» поиском.

Многомерная условная оптимизация: Метод штрафов. Метод прямого поиска с возвратом. Метод проектирования градиента.

Постановка: требуется оптимизировать х (формальная постановка)

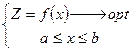
- функция одной переменной

- целевая функция.

Решение: найти х, при котором принимает оптимальное значение.

2 варианта:

- минимизировать – задача минимизации;

- максимизировать – задача максимизации.

Рассмотрим случай минимизации

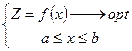
2 способа:

- аналитический

- численный

В аналитическом задается в виде формулы, в численном задается в виде черного ящика, на входе подается х, на выходе значение целевой функции в этой точке.

Пусть функция определена в некоторой области S (), в случае одномерной оптимизации S – интервал :

1. точка называется глобальным минимумом, если для