Реферат: Конспект по дискретной математики
3) если прямые совпадают, то множество пересечений = множество прямой.
Пересечение системы множеств: 
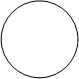
4) Разностью 2-х множеств А и В называется множество, состоящее из всех элементов А, не входящих в В.
С = А \ В
 |  | |
|
A \ B
|
А \ В
|
|
|
|
|
A = {a,b,d}; B = {b,c,d,h} C = A \ B={a}.
В отличии от предыдущих операций разность: 1) строго двухместна;
2) не коммутативна, т.е. A\B¹B\A.
4) дополнение 
E – универсальное множество.
-- дополнение
Операции объединения, пересечения и дополнения называются Булевыми.
Основные законы операций над множествами.
Некоторые свойства È, Ç похожи на алгебраические операции, однако многие свойства операций над множествами все же отличаются.
Основные свойства
1) AUB = BUA ; A Ç B = B Ç A –переместительный закон объединения и пересечения.
2) ( А UB)UC = AU(BUC); (A Ç B) Ç C=A Ç (B Ç C) – сочетательныйзакон.
3) А U Æ =A, A ÇÆ = Æ , A \ Æ =A, A \ A= Æ
1,2,3 – есть аналог в алгебре.
3.а) Æ \ A = Æ - нет аналога.
4) 
Æ; E \ A =; A \ E=Æ; AUA=A; AÇA=A; AUE=E; AÇE=A;
5.а) свойства 1-4 очевидны и не нуждаются в доказательствах.
5) A Ç ( BUC )=( A Ç B )( A Ç C ) – есть аналогичный распределительный закон Ç относительно U.
Прямые произведения и функции
Прямым декартовым “х” множеством А и В называется множество всех пар (a;b), таких, что аÎА, bÎB.
С=AхВ, если А=В то С=А2 .
Прямыми «х» n множеств A1 x,…,xAn называется множество векторов (a1 ,…an ) таких, что a1 ÎA1 ,…, An ÎAn .
Через теорию множеств введем понятие функции.
Подмножество FÎMx xMy называется функцией, если для каждого элемента хÎMx найдется yÎМу не более одного.
(x;y)ÎF, y=F(x).
Соответствие между аргументом и функцией можно изобразить с помощью диаграммы Венна:
 |
 |
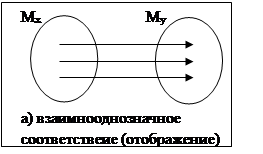
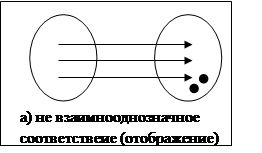