Реферат: Конспект по дискретной математики

Пример: 1) (х,у) в круге

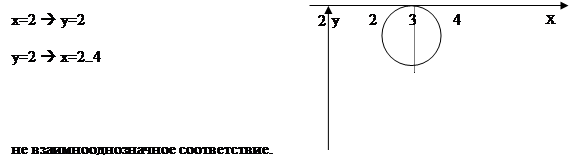2) x = sinx
R- R

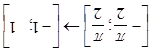
Пусть даны две функции f: A-B и g: B-C, то функция y:A-C называется композицией функций f и g.

Y=fogo – композиция.

Способы задания функций:

1) таблицы, определены для конечных множеств;

2) формула;

3) графики;

Способы 1-3 частные случаи выч. процедуры.

Пример процедуры, не относящейся к 3 способам задания функций n!

Взаимнооднозначное соответствие и мощности множеств.

Определение: Множества равномощны |A|=|B| если между ними взаимнооднозначное соответствие.

Теорема: Если для конечного множества А мощность равна |A| то количество всех подмножеств 2^{| A |} =2ⁿ .

Множества равномощные N называются счетными, т.е. в них можно выполнить нумерацию элементов. N – множество натуральных чисел.

Множество N² – счетно.

Доказательство

Разобьем N² на классы

К 1-ому классу отнесем N₁ (1; 1)

1-ый элемент 1-го множества

1-ый элемент 2-го множества

Ко 2-му классу N₂ {(1;2), (2;1)}

К i-му классу N_i {(a;b)| (a+b=i+1}

Каждый класс будет содержать i пар.

Упорядоченный классы по возрастанию индекса i, а пары внутри класса упорядоченные по направлению первого элемента а.

Занумеруем последовательность классов, что и доказывает счетность множества N² .

Аналогично доказывается счетность множеств N³ ,…,N^k .

Теорема Кантора:

Множество всех действительных чисел на отрезке [0;1] не является счетным.

Доказательство

Допустим это множество счетно изобразим его числа десятичными дробями.

}

1

1-? 0, a₁₁ , a₁₂ ?.

2-я 0, а₂₁ , a₂₂ ….