Реферат: Кривые второго порядка

Эксцентриситетом эллипса e называют отношение межфокусного расстояния 2с к длине большой оси 2а .

(7)

Следовательно, причем когда т. е. имеем окружность.

При стремящемся к 1 эллипс становится более вытянутым вдоль оси Ох .

Выразим фокальные радиусы точки через эксцентриситет. Из (4):

(8)

Из (3):

Значит, подставив координаты точки эллипса в уравнения (8), получаем фокальные радиусы точки М .

Прямые называются директрисами эллипса .

– левая директриса,

– правая директриса.

Заметим, что директрисы эллипса обладают следующим важным свойством:

(9)

т. е. отношение расстояния r_i от любой точки эллипса до фокуса к расстоянию d_i от нее до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса.

2 Гипербола

Гиперболой называется множество точек плоскости, для каждой из которых модуль разности расстояний от которых до двух данных точек той же плоскости, называемых фокусами гиперболы, есть заданная постоянная величина меньшая , чем расстояние между фокусами

Пусть фокусы гиперболы лежат на оси Ох , причем т. е. Заметим, что

Пусть – произвольная точка гиперболы. Как и ранее, – фокальные радиусы точки М .

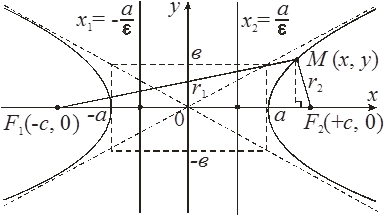
По определению гиперболы:

где

Следовательно,

(10)

Умножим (10) на

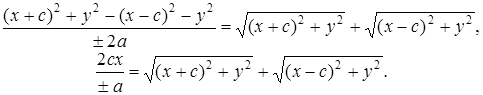(11)

Сложим уравнения (10) и (11):

(12)