Реферат: Кривые второго порядка

Каноническое уравнение эллипса имеет вид

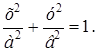
Так как эллипс проходит через точку М , то ее координаты должны удовлетворять этому уравнению

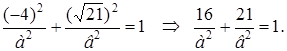
Фокусы находятся на оси Ох , следовательно

Объединив полученные два уравнения в систему, найдем а ² и в ² :

Следовательно, уравнение данного эллипса имеет вид:

Фокальные радиусы точки М определим по формулам (8): х = –4, , .

Þr ₁ = а + eх = = 8 – 3 = 5,

r ₂ = а – eх = = 8 + 3 = 11.

ПРИМЕР 3

Определить траекторию точки М , которая при своем движении остается вдвое ближе к точке F (–1; 0), чем к прямой х = –4.

Решение.

Пусть М (х , у ). Тогда çMN ú = 2 çMF ú, çMN ú = ç–4 – x ú, çMF ú= = , Þç– (4 + х )ú = .

Возведем в квадрат: (4 + х )² = 4 ((х + 1)² + у ² ),

Þ 16 + 8х + х ² = (х ² + 2х + 1 + у ² ) · 4 = 4х ² + 8х + 4 + 4у ² ,

Þ 3х ² + 4у ² = 12 ÞÞ.

Таким образом, точка М (х , у ) движется по эллипсу.

ПРИМЕР 4

Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса .

Решение.

Из уравнения данного эллипса имеем: а = 5; в = 3, а > в .

Следовательно, Поэтому, вершинами эллипса будут точки (±5; 0), (0; ±3), а фокусами точки F ₁ (–с ; 0) = (–4; 0), F ₂ (4; 0).

Так как фокусы эллипса находятся на оси Ох (а > в ), то вершины (±5; 0) будут фокусами гиперболы. Каноническое уравнение гиперболы, имеющей фокусы на оси Ох , имеет вид (13)

,