Реферат: Кривые второго порядка

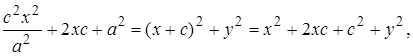
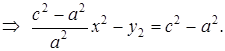
Пусть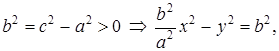

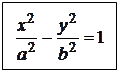(13)

(13) – каноническое уравнение гиперболы с центром в начале координат. Соответственно, уравнение

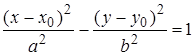
– каноническое уравнение гиперболы с центром в точке

Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Гипербола с равными полуосями (a = b ) называется равносторонней, ее каноническое уравнение имеет вид:

Точки называются вершинами гиперболы.

Заметим, что если уравнение гиперболы имеет вид

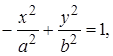(14)

то фокусы гиперболы находятся на оси Оу , а ветви гиперболы будут направлены не влево и вправо, а вверх и вниз.

Так как , то (15)

Как и в случае с эллипсом, эксцентриситетом гиперболы называется отношение межфокусного расстояния к длине действительной оси :

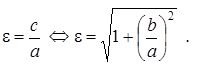(16)

Следовательно,

Выразим фокальные радиусы точки через эксцентриситет. Из (12)

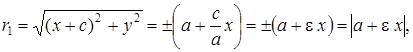
(17)

Прямые называются директрисами гиперболы.

– левая директриса,

– правая директриса.

Директрисы гиперболы обладают тем же свойством, что и директрисы эллипса

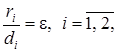(18)

т. е. отношение расстояния от любой точки гиперболы до фокуса к расстоянию от нее до соответствующей директрисы есть величина постоянная, равная эксцентриситету гиперболы.

Для гиперболы важную роль играют также прямые

(19)

которые являются ее асимптотами , т. е. прямыми к которым график гиперболы неограниченно близко приближается, но не пересекает их. Заметим, что асимптоты гиперболы совпадают с диагоналями прямоугольника (если их продолжить)

Следует отметить, что если уравнение гиперболы имеет вид (14), т. е. ее фокусы находятся на оси Оу , то изменятся формулы для вычисления фокальных радиусов, эксцентриситета, директрис. Так – эксцентриситет, – уравнения директрис.

3 Парабола