Реферат: Лекции по Линейной алгебре

(продолжение)

6. Реализация абстрактной группы как группы преобразований.

Существует несколько способов связать с данной абстрактной группой некоторую группу преобразований. В дальнейшем, если не оговорено противное, знак алгебраической операции в абстрактной группе будет опускаться.

Пусть некоторая подгруппа.

А) Для каждого определим отображение (левый сдвиг на элемент h) формулой .

Теорема 1

1. 

2. Множество L(H,G)= является группой преобразований множества G.

3. Соответствие: является изоморфизмом групп H и L(H,G).

Доказательство.

1. Надо проверить, что отображение взаимно однозначно для всякого . Если , то по закону сокращения. Значит инъективно. Если любой элемент, то и так что к тому же и сюръективно.

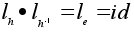2. Обозначим через · операцию композиции в группе Sym(G) взаимно однозначных отображений . Надо проверить, что и . Пусть любой элемент. Имеем: ; и значит, .

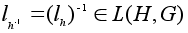3. Пусть 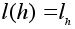. Надо проверить, что l взаимно однозначно и сохраняет операцию. По построению l сюръективно. Инъективность вытекает из закона правого сокращения: 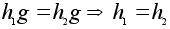. Сохранение операции фактически уже было установлено выше: .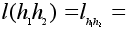

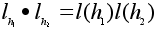Следствие.

Любая абстрактная группа изоморфна группе преобразований некоторого множества (Достаточно взять G=H и рассмотреть левые сдвиги).

Для случая конечных групп получается теорема Кэли:

Любая группа из n элементов изоморфна подгруппе группы подстановок степени n.

2. Для каждого определим отображение 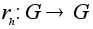(правый сдвиг на элемент h) формулой .

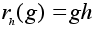Теорема B.

1. .

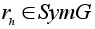2. Множество 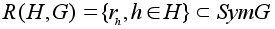является группой преобразований множества G.

3. Соответствие 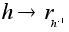является изоморфизмом групп H и R(H,G).

Доказательство теоремы B вполне аналогично доказательству теоремы A. Отметим только, что . Именно поэтому в пункте 3 теоремы В появляется не , а .

С) Для каждого определим (сопряжение или трансформация элементом h ) формулой .

Теорема С.

1. Каждое отображение 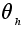является изоморфизмом группы G с собой (автоморфизмом группы G).

2. Множество 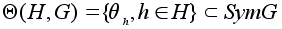является группой преобразований множества G.

3. Отображение 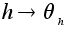сюръективно и сохраняет операцию.

Доказательство.

1. Поскольку 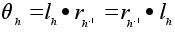, отображение 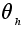взаимно однозначно как композиция двух отображений такого типа. Имеем: 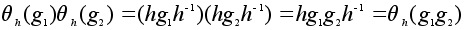и потому 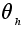сохраняет операцию.