Реферат: Лекции по Линейной алгебре

В рассмотренной выше группе подгруппа не является нормальной так как левые и правые смежные классы не совпадают. Сопряженными с H будут подгруппы и .

Если - любая подгруппа, то ее централизатор Z = Z(H,G) - нормальная подгруппа в G , так как для всех ее элементов z . В частности, центр Z(G) любой группы G -нормальная подгруппа.

Подгруппа H индекса 2 нормальна. В самом деле, имеем 2 смежных класса : H и Hg = G-H = gH.

Теорема (свойство смежных классов по нормальной подгруппе).

Если подгруппа H нормальна в G, то множество всевозможных произведений элементов из двух каких либо смежных классов по этой подгруппе снова будет одним из смежных классов, то есть .

Доказательство.

Очевидно, что для любой подгруппы H .Но тогда

= = = .

Таким образом, в случае нормальной подгруппы H определена алгебраическая операция на множестве смежных классов. Эта операция ассоциативна поскольку происходит из ассоциативного умножения в группе G. Нейтральным элементом для этой операции является смежный класс . Поскольку , всякий смежный класс имеет обратный. Все это означает, что относительно этой операции множество всех (левых или правых) смежных классов по нормальной подгруппе является группой. Она называется факторгруппой группы G по H и обозначается G/H. Ее порядок равен индексу подгруппы H в G.

Абстрактная теория групп

(продолжение)

9 Гомоморфизм.

Гомоморфизм групп - это естественное обобщение понятия изоморфизма.

Определение.

Отображение групп называется гомоморфизмом, если оно сохраняет алгебраическую операцию, то есть : .

Таким образом, обобщение состоит в том, что вместо взаимно однозначных отображений, которые участвуют в определении изоморфизма, здесь допускаются любые отображения.

Примеры.

1. Разумеется, всякий изоморфизм является гомоморфизмом.

2. Тривиальное отображение является гомоморфизмом.

3. Если - любая подгруппа, то отображение вложения будет инъективным гомоморфизмом.

4. Пусть - нормальная подгруппа. Отображение группы G на факторгруппу G/H будет гомоморфизмом поскольку . Этот сюръективный гомоморфизм называется естественным.

5. По теореме С предыдущего раздела отображение сопряжения сохраняет операцию и, следовательно является гомоморфизмом.

6. Отображение , которое каждому перемещению n- мерного пространства ставит в соответствие ортогональный оператор (см. лекцию №3) является гомоморфизмом поскольку по теореме 4 той же лекции .

Теорема (свойства гомоморфизма)

Пусть - гомоморфизм групп, и - подгруппы. Тогда:

1. , .

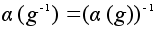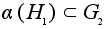2. - подгруппа.

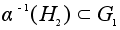3. -подгруппа, причем нормальная, если таковой была .