Реферат: Лекции по Линейной алгебре

Пусть p = a(h) , q = a(k) . Тогда и . По признаку подгруппы получаем 2.

Пусть то есть элементы p = a(h) , q = a(k) входят в . Тогда то есть . Пусть теперь подгруппа нормальна и - любой элемент. и потому .

Определение.

Нормальная подгруппа называется ядром гомоморфизма .Образ этого гомоморфизма обозначается .

Теорема.

Гомоморфизм a инъективен тогда и только тогда, когда

Доказательство.

Поскольку , указанное условие необходимо. С другой стороны, если , то и если ядро тривиально, и отображение инъективно.

Понятие гомоморфизма тесно связано с понятием факторгруппы.

Теорема о гомоморфизме.

Любой гомоморфизм можно представить как композицию естественного (сюръективного) гомоморфизма , изоморфизма и (инъективного) гомоморфизма (вложения подгруппы в группу): .

Доказательство.

Гомоморфизмы p и i описаны выше (см. примеры) Построим изоморфизм j. Пусть . Элементами факторгруппы являются смежные классы Hg . Все элементы имеют одинаковые образы при отображении a : . Поэтому формула определяет однозначное отображение . Проверим сохранение операции .Поскольку отображение j очевидно сюръективно, остается проверить его инъективность. Если , то и потому . Следовательно, и по предыдущей теореме j инъективно.

Пусть - любой элемент. Имеем : . Следовательно, .

10 Циклические группы.

Пусть G произвольная группа и - любой ее элемент. Если некоторая подгруппа содержит g , то она содержит и все степени . С другой стороны, множество очевидно является подгруппой G .

Определение.

Подгруппа Z(g) называется циклической подгруппой G с образующим элементом g. Если G = Z(g) , то и вся группа G называется циклической.

Таким образом, циклическая подгруппа с образующим элементом g является наименьшей подгруппой G, содержащей элемент g.

Примеры

1. Группа Z целых чисел с операцией сложения является циклической группой с образующим элементом 1.

2. Группа 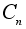поворотов плоскости на углы кратные 2p¤n является циклической с образующим элементом 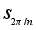- поворотом на угол 2p¤n. Здесь n = 1, 2, ...

Теорема о структуре циклических групп.

Всякая бесконечная циклическая группа изоморфна Z. Циклическая группа порядка n изоморфна Z / nZ .

Доказательство.

Пусть G = Z(g) - циклическая группа. По определению, отображение - сюръективно. По свойству степеней и потому j - гомоморфизм. По теореме о гомоморфизме . H = KerjМZ. Если H - тривиальная подгруппа, то . Если H нетривиальна, то она содержит положительные числа. Пусть n - наименьшее положительное число входящее в H. Тогда nZМH. Предположим, что в H есть и другие элементы то есть целые числа не делящееся на n нацело и k одно из них. Разделим k на n с остатком: k = qn +r , где 0 < r < n. Тогда r = k - qn О H , что противоречит выбору n. Следовательно, nZ = H и теорема доказана.

Отметим, что » Z / nZ .

Замечание.