Реферат: Лекции по Линейной алгебре

Абстрактная теория групп

1. Понятие абстрактной группы.

1.Понятие алгебраической операции.

Говорят, что на множестве X определена алгебраическая операция (*), если каждой упорядоченной паре элементов поставлен в соответствие некоторый элемент называемый их произведением.

Примеры.

1. Композиция перемещений на множествах является алгебраической операцией.

2. Композиция подстановок является алгебраической операцией на множестве всех подстановок степени n.

3. Алгебраическими операциями будут и обычные операции сложения, вычитания и умножения на множествах соответственно целых, вещественных и комплексных чисел. Операция деления не будет алгебраической операцией на этих множествах, поскольку частное 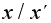не определено при 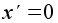. Однако на множествах 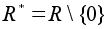, 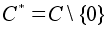это будет алгебраическая операция.

4. Сложение векторов является алгебраической операцией на множестве .

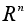5. Векторное произведение будет алгебраической операцией на множестве .

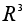6. Умножение матриц будет алгебраической операцией на множестве всех квадратных матриц данного порядка.

2.Свойства алгебраических операций.

1. Операция (*) называется ассоциативной, если .

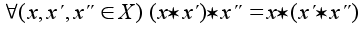Это свойство выполняется во всех приведенных выше примерах, за исключением операций вычитания ( и деления) и операции векторного умножения векторов. Наличие свойства ассоциативности позволяет определить произведение любого конечного множества элементов. Например, если , . В частности можно определить степени с натуральным показателем: . При этом имеют место обычные законы: , .

2. Операция (*) называется коммутативной, если

В приведенных выше примерах операция коммутативна в примерах 3 и 4 и не коммутативна в остальных случаях. Отметим, что для коммутативной операции

3. Элемент 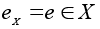называется нейтральным для алгебраической операции (*) на множестве X, если 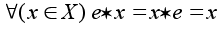. В примерах 1-6 нейтральными элементами будут соответственно тождественное перемещение, тождественная перестановка, числа 0 и 1 для сложения и умножения соответственно (для вычитания нейтральный элемент отсутствует !), нулевой вектор, единичная матрица. Для векторного произведения нейтральный элемент отсутствует. Отметим, что нейтральный элемент (если он существует) определен однозначно. В самом деле, если 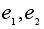- нейтральные элементы, то 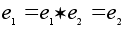. Наличие нейтрального элемента позволяет определить степень с нулевым показателем: .

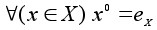4. Допустим, что для операции (*) на X существует нейтральный элемент. Элемент 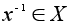называется обратным для элемента 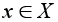, если 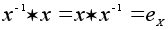. Отметим, что по определению 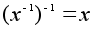. Все перемещения обратимы также как и все подстановки. Относительно операции сложения все числа обратимы, а относительно умножения обратимы все числа, кроме нуля. Обратимые матрицы - это в точности все матрицы с ненулевым определителем. Если элемент x обратим, то определены степени с отрицательным показателем: 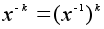. Наконец, отметим, что если x и y обратимы, то элемент 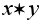также обратим и 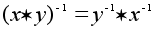. (Сначала мы одеваем рубашку, а потом куртку; раздеваемся же в обратном порядке!).

Определение (абстрактной) группы.

Пусть на множестве G определена алгебраическая операция (*). (G ,*) называется группой, если

1. Операция (*) ассоциативна на G.

2. Для этой операции существует нейтральный элемент e (единица группы).

3. Каждый элемент из G обратим.

Примеры групп.

1. Любая группа преобразований.

2. (Z, +), (R, +), (C, +).

3. 

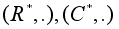
4. Матричные группы: 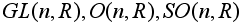- невырожденные квадратные матрицы порядка n, ортогональные матрицы того же порядка, ортогональные матрицы с определителем 1.

5. Простейшие свойства групп.

6. В любой группе выполняется закон сокращения: 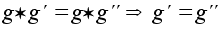(левый закон сокращения; аналогично, имеет место и правый закон). Доказательство. Домножим равенство слева на 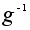и воспользуемся свойством ассоциативности: .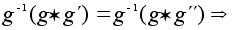

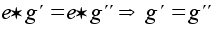7. --> ЧИТАТЬ ПОЛНОСТЬЮ <--