Реферат: Линейная Алгебра. Теория групп

Элемент называется обратным для элемента x, если

(4)

Для сложения чисел обратный элемент существует для любого числа и равен противоположному числу. Для умножения обратный элемент так и называется и существует у любого числа, кроме 0. В случае умножения матриц обратный элемент равен обратной матрице и существует в том случае, если эта матрица невырождена, то есть ее определитель не равен нулю.

Элементы для которых существует обратный называются обратимыми. Из условия (4) сразу вытекает, что элемент всегда обратим и обратным для него будет исходный элемент x. Кроме того в случае ассоциативной операции произведение двух обратимых элементов снова будет обратимым элементом и при этом . В самом деле: и аналогично

Если элемент определен однозначно, можно определить степени x с отрицательным целым показателем, а именно:

, где m=1,2,... . При этом сохраняются обычные правила действий со степенями.

Замечание

В конкретных алгебраических системах алгебраическая операция чаще всего обозначается либо знаком (+) и называется сложением , либо знаком (.) и называется умножением. В первом случае говорят об аддитивном, а во втором о мультипликативном способе записи операции. Операция записанная аддитивно как правило считается коммутативной. В этом случае вместо термина «обратный» используется термин «противоположный элемент», который, естественно, обозначается (-x), а вместо степени элемента говорят о его кратных (nx).

Понятие группы

Определение

Множество G на котором определена бинарная операция (*) называется группой (G,*), если выполняются условия:

1. Операция (*) ассоциативна.

2. Для операции существует нейтральный элемент.

3. Все элементы G обратимы.

Примеры групп

1. R - группа действительных чисел с операцией сложения. ( аддитивная группа действительных чисел)

2. C - аддитивная группа комплексных чисел.

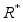3. - группа ненулевых действительных чисел с операцией умножения ( мультипликативная группа действительных чисел)

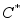4. - мультипликативная группа комплексных чисел.

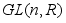5. - группа невырожденных матриц порядка n с действительными элементами. (Аналогично, )

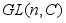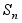6. - группа перестановок множества 1,2, ..., n.

Во всех этих примерах наличие свойств 1- 3 не вызывает сомнений.

Прежде чем приводить другие примеры групп укажем некоторые простейшие свойства этих алгебраических систем. Во всех последующих формулировках считается, что x, y, z, ... - элементы некоторой группы G.

1. Закон сокращения

(левое сокращение)

(правое сокращение)

Докажем, например, первый закон. Используем существование обратного элемента и свойство ассоциативности операции.