Реферат: Линейная Алгебра. Теория групп

Неприводимые многочлены над некоторыми полями.

1. Поле комплексных чисел C. Имеет место фундаментальная теорема Гаусса: Всякий многочлен положительной степени над полем C имеет корень. Из нее вытекает, что над полем C неприводимы только многочлены первой степени.

2. Поле вещественных чисел R. Чтобы перейти от поля C к полю R, заметим, что отображение , сопоставляющее каждому комплексному числу z сопряженное число является изоморфизмом поля на себя (автоморфизмом ) и переводит поле R в себя. Отсюда вытекает, что для всякого и всякого имеет место формула: = (), где - многочлен с комплексно сопряженными коэффициентами. Пусть теперь - многочлен положительной степени. По теореме Гаусса он имеет корень. Но, ) = 0. 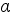Если , то многочлены ( x - ) и ( x - ) взаимно просты и из делимости многочлена p ( по теореме Безу) на ( x - 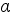) и на ( x - ) следует его делимость на их произведение . Следовательно, над полем R неприводимыми будут , во первых, все многочлены первой степени, а, во-вторых, те многочлены второй степени, которые не имеют корней в R ( то есть у которых дискриминант отрицателен). Все прочие многочлены - приводимы.

3. Поле рациональных чисел Q.

Если q ненулевой многочлен с рациональными коэффициентами, то, приводя их к общему знаменателю, можно записать: q = () = , где все коэффициенты целые числа, ОНД() = 1 и ,>0 . Легко видеть, что многочлен и число определены однозначно. Будем называть примитивным многочленом, соответствующим многочлену q.

Лемма : .

Для всякого целочисленного многочлена w = и простого числа p обозначим через многочлен над полем GF(p), коэффициенты которого получаются из соответствующих коэффициентов w приведением по модулю p : . Очевидно, что отображение является гомоморфизмом кольца Z[x] в кольцо GF(p)[x]. Многочлен w будет примитивным тогда и только тогда, когда для любого p . Поскольку в кольце GF(p)[x] нет делителей нуля, отсюда и вытекает утверждение леммы.

Таким образом вопрос о приводимости многочлена над полем рациональных чисел сводится к вопросу о разложении на множители меньшей степени многочлена с целыми коэффициентами. В этом направлении имеется следующее достаточное условие неприводимости:

Критерий Эйзенштейна.

Если для многочлена q с целыми коэффициентами q = удается найти такое простое число p, что

1.ОНД( p , ) = 1 2. 3. не делит то этот многочлен неприводим.

Доказательство.

Предположим, что q приводимый многочлен : q = uv. Тогда . По условию теоремы =a, где a 0. Значит, , , где k ), равный делится РЅР° , что противоречит условию.

Примеры.

1. Многочлен 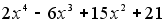неприводим над полем Q. Достаточно взять p = 3 и применить критерий Эйзенштейна.

2. Для всякого n>0 многочлен неприводим над Q. Достаточно взять p=2 в предыдущей теореме. Отсюда вытекает, что над полем рациональных чисел существуют неприводимые многочлены любой степени.

   
   

4. Случай конечного поля GF(q).

Особенностью этого случая является тот факт, что имеется только конечное число многочленов данной степени и, в частности, неприводимых многочленов. Будем рассматривать унитарные многочлены степени n над GF(q). Такой многочлен имеет вид: , где , . Значит, количество таких многочленов Обозначим через количество унитарных неприводимых многочленов степени n . Можно указать алгоритм, позволяющий последовательно перечислять все такие многочлены в порядке возрастания их степеней. Для n=1 все многочлены (x - a ) неприводимы, поэтому . Если все неприводимые многочлены степени меньше n уже перечислены, составим всевозможные произведения некоторых степеней таких многочленов, так чтобы эти произведения имели степень n. Все те многочлены степени n, которые не вошли в это множество, и будут неприводимыми многочленами степени n. Разумеется, практическое применение этого алгоритма требует умения совершать арифметические действия в поле GF(q). Кроме того, количество вычислений быстро растет с ростом n (а также q ). В следующей таблице указаны некоторые неприводимые многочлены над полями GF(p) для простых p = 2,3,5.

	P=2	p=3	p=5
« 1 2 3 4 5 6 7 » К-во Просмотров: 384 Бесплатно скачать Реферат: Линейная Алгебра. Теория групп >>> Скачать <<< Меню Поиск