Реферат: Линейная Алгебра. Теория групп
y=z.
-
Единственность нейтрального элемента
В любой группе нейтральный элемент определен однозначно. В самом деле, если 
и 
оба являются нейтральными, то по определению
и в то же время 
, откуда 
. Единственный нейтральный элемент группы G будет в дальнейшем обозначаться 
или просто e.
-
Единственность обратного элемента
Для каждого элемента x обратный элемент 
определен однозначно. В самом деле, если элементы y и z являются обратными для x, то y*x=e и z*x=e, откуда y*x=z*x и по закону сокращения y=z.
-
Признак нейтрального элемента
Действительно, поскольку 
, имеем 
, откуда по закону сокращения получаем 
.
-
Разрешимость любого уравнения первой степени (существование обратной операции)
. Элемент z определен однозначно. (Его можно назвать «частным» от деления y на x).
Имеем: 
и значит можно взять 
. Однозначность следует из закона сокращения: 
.
Понятие подгруппы
Определение
Группа 
называется подгруппой группы 
, если, во первых
(как подмножество) и, во-вторых,
(то есть закон умножения на подмножестве H такой же как и во всем множестве G.)
Тот факт, что является подгруппой в обозначается с помощью символа включения: 
или просто .
Примеры подгрупп.
-
Целые числа с операцией сложения (Z) образуют подгруппу в группе R, которая, в свою очередь является подгруппой группы C.
-
Четные перестановки образуют подгруппу
в группе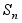 
всех перестановок. -
Матрицы с определителем 1 образуют подгруппу
в группе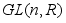 
всех невырожденных матриц.
Чтобы проверить, будет ли данное подмножество H в G подгруппой надо, очевидно, проверить следующие условия :
-
-
-
.
Оказывается, что вместо трех этих условий достаточно проверить только одно.