Реферат: Математическое моделирование электропривода

, (2)

где - постоянная времени, - декремент затухания колебаний. В случае же длительность процесса в системе (2) равна .

Запишем уравнение (1) в следующем виде

. (3)

Тогда уравнения замкнутой системы будут иметь вид

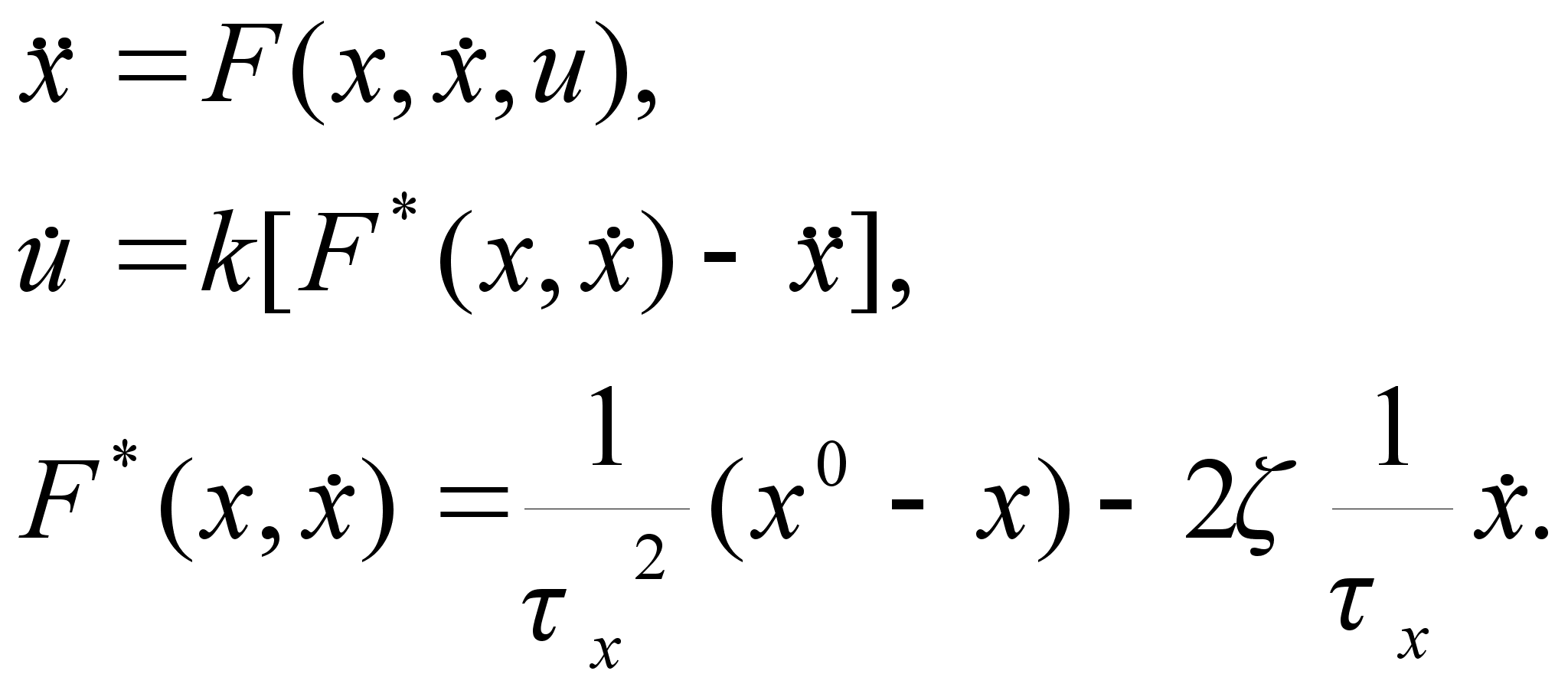(4)

Параметры эталонной системы известны. Коэффициент ускорения контура ускорения подлежит определению из условия, чтобы процесс в синтезируемой системе (4) проходил в окрестности решения уравнения (2). Искомое значение можно найти по формуле

,

где находят из (3)

, , .

Отсюда, подставляя значение производных в точке , имеем

(5)

По этому соотношению можно вычислить требуемый коэффициент усиления для заданных значений , если назначена величина .

В Таблица 1 представлены соотношения , соответствующие различным значениям параметра для случая, когда усиление в контуре ускорения принято равным и . В соответствии с (5) величина , при расчетах принималось .

Таблица 1

	0,2	0,4	0,6	0,8	1,0	3,0
	4,4	4,3	4,2	4,1	4,0	3,0	9
	3,0	2,9	2,8	2,7	2,6	1,6	6,2

Видно что в алгоритме управления с усилением отношение постоянных времени при изменении параметра в пределах . Это свидетельствует о слабой параметрической чувствительности системы (4). Напротив, если принять , то при изменении в указанном диапазоне соотношение между постоянными времени (по управляемой переменной) и (контура ускорения) будет меньше трех. В данном случае процесс будет заметно отличаться от эталонного при .

В Таблица 2 приведены числовые данные, показывающие зависимость перерегулирования от . Эти данные соответствуют переходной характеристике системы для случая . Коэффициент усиления изменялся таким образом, что отношение было равным значением,

Таблица 2

указанным в верхней строке таблицы. Как следует из приведенных данных, заметное отклонение от переходной характеристики эталонной системы наблюдается при . В случае величина исчезающе мала, но переходный процесс завершается за время , что соответствует эталонной системе (2).

2.Математическое моделирование

1. Построение уравнения

Синтезируем алгоритм управления по линейной модели. В практике проектирования приводных систем различного назначения часто используются именно такие модели. Это позволит синтезировать структуру и найти приближенные значения параметров алгоритмов управления. Часто оказывается, что найденные таким образом параметры обеспечивают выполнение требований, предъявленных к системе. Итак, решение задачи синтеза алгоритмов управления по линейным моделям представляет практический интерес.

Общепринятые уравнения исполнительного двигателя имеют вид

(6)

где - ток, - индуктивность якорной цепи.

Процессы в электрических цепях двигателя протекают существенно быстрее, чем в механических. Поэтому обычно пренебрегают влиянием цепи с передаточной функцией