Реферат: Математическое моделирование электропривода
и интегрируя обе части равенства по времени. В этом случае уравнения замкнутого контура будут
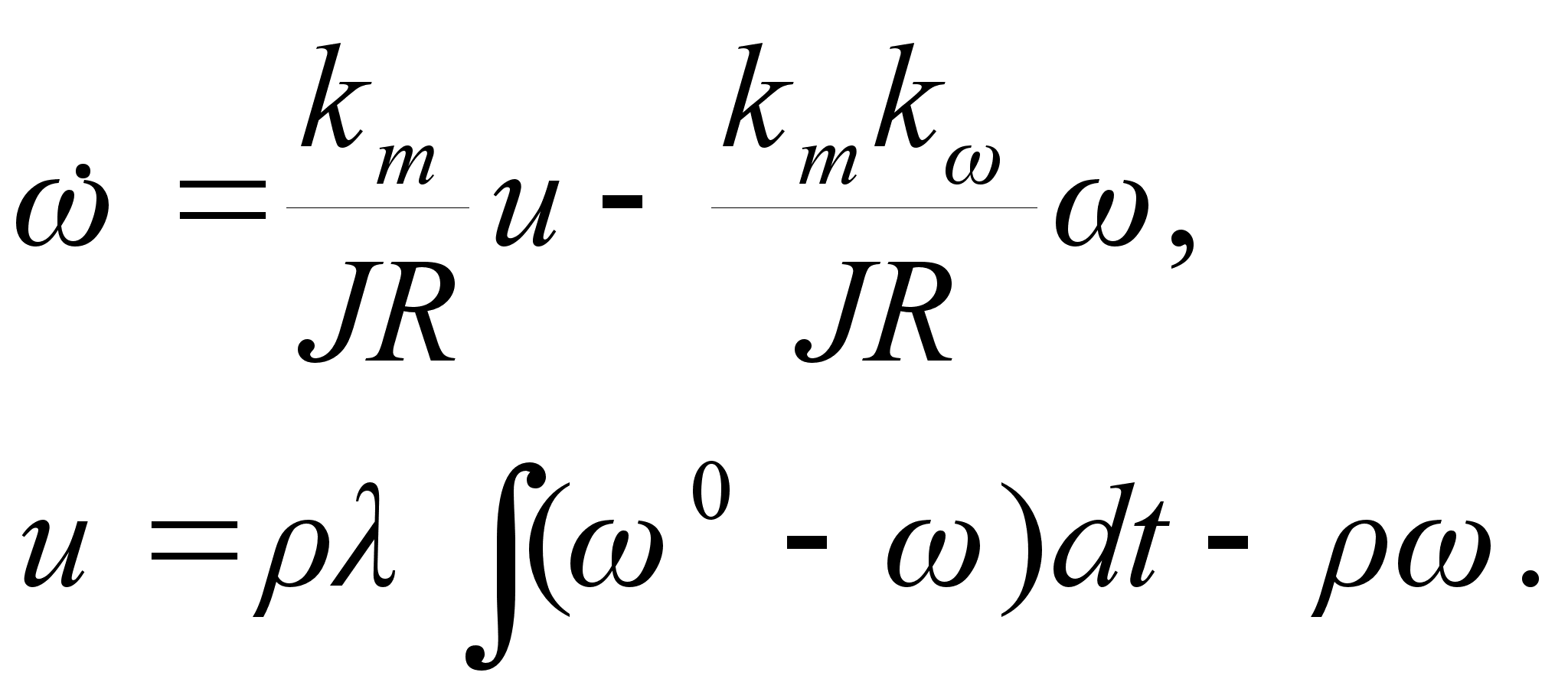(17)
Построим теперь алгоритм управления углом поворота вала двигателя(угловым положением). Примем, что контур управления угловой скоростью синтезирован и его параметры 
расчитываются из условия, чтобы процесс изменения 
подчинялся (16.1). Получаем, что исходными уравнениями управляемого процесса будут
(18)
где 
- угол поворота вала системы, связанного с валом двигателя через редуктор с передаточным отношением 
. Требуется синтезировать алгоритм управления, который обеспечивает поворот вала двигателя на угол 
таким образом, чтобы ошибка рассогласования 
подчинялась кинематическому закону
(18.1)
Управляющей функцией в данном случае выступает величина 
, которая является задающим воздействием для контура угловой скорости.
Запишем уравнение (18) в виде
(19)
Подставим вместо 
выражение для 
из (18.1). Получим программную управляющую функцию
и закон управления с обратной связью
(20)
Подставляя (18) в (20) получим
(21)
Потребуем, чтобы решение этого уравнения соответствовало процессу в эталонной системе
(22)
где 
- постоянная времени по регулируемой переменной. Эта величина при проектировании задается. Для наилучшего переходного процесса 
постоянная времени примерно в 3 раза превосходит величину 
. Поэтому для расчета параметров 
, учитывая (21) и (22) будут справедливы соотношения
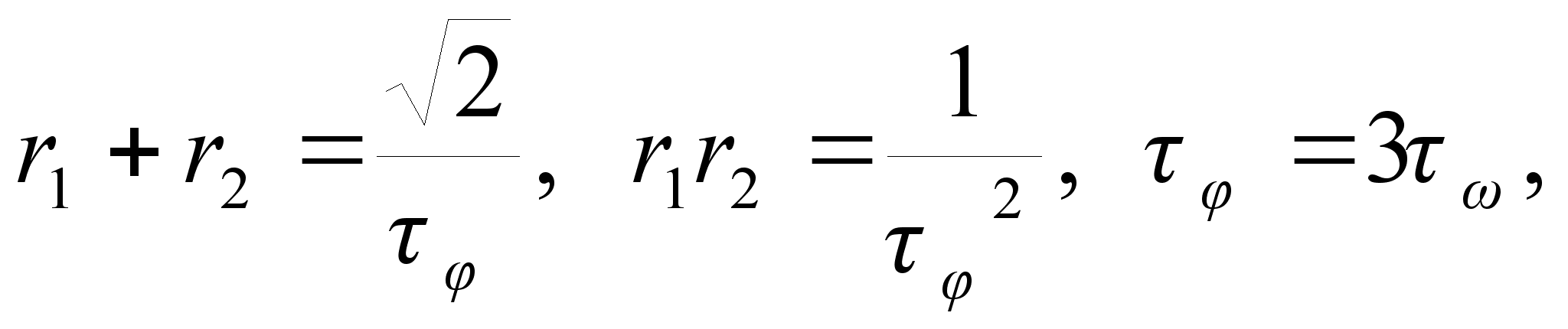(23)
которые представляют собой уравнения относительно 
. Следовательно, на основании (20) можно записать
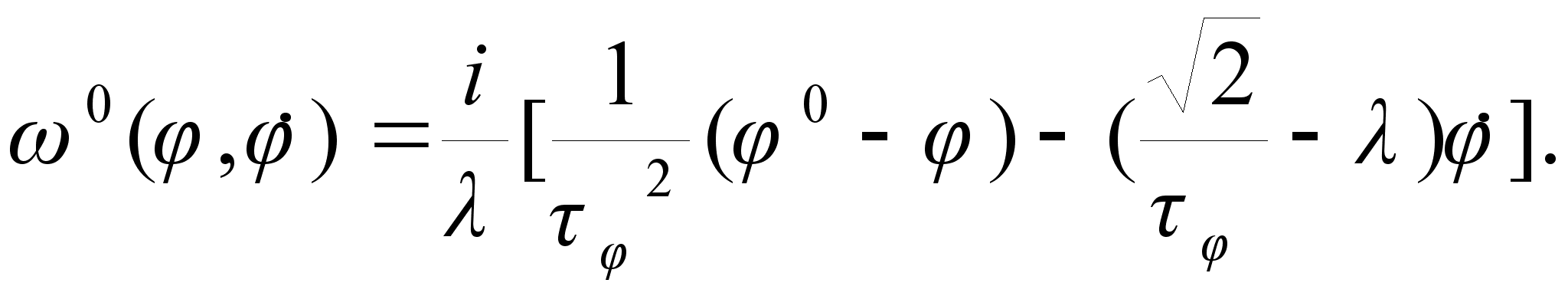(24)
Проведенное рассмотрение исчерпывает задачу построения алгоритмов управления угловой скоростью и углом поворота вала двигателя. Все необходимые уравнения для последующей работы были построены.
Определение свойств системы
Определение свойств динамической системы - это нахождение особых точек системы и анализ устойчивости положения равновесия.
Для нахождения положений равновесия используем уравнение
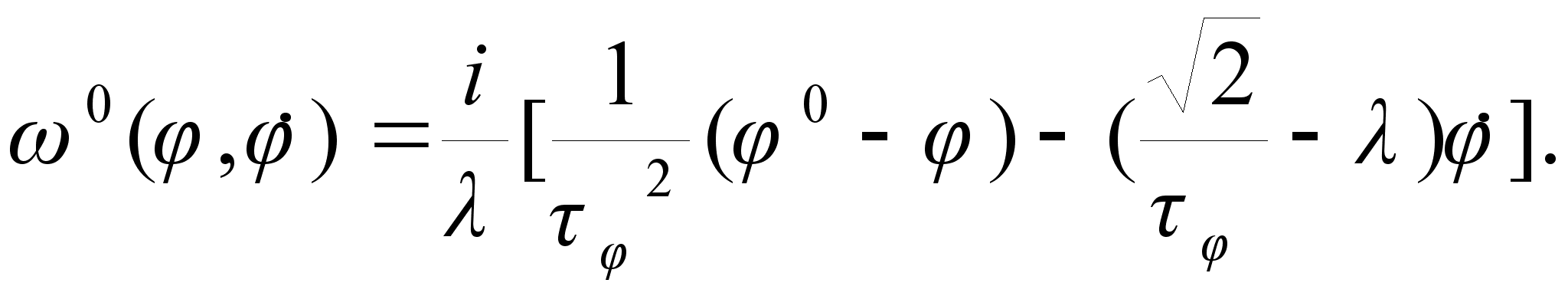
Приравняем нулю 
и подставим в наше уравнение, получим
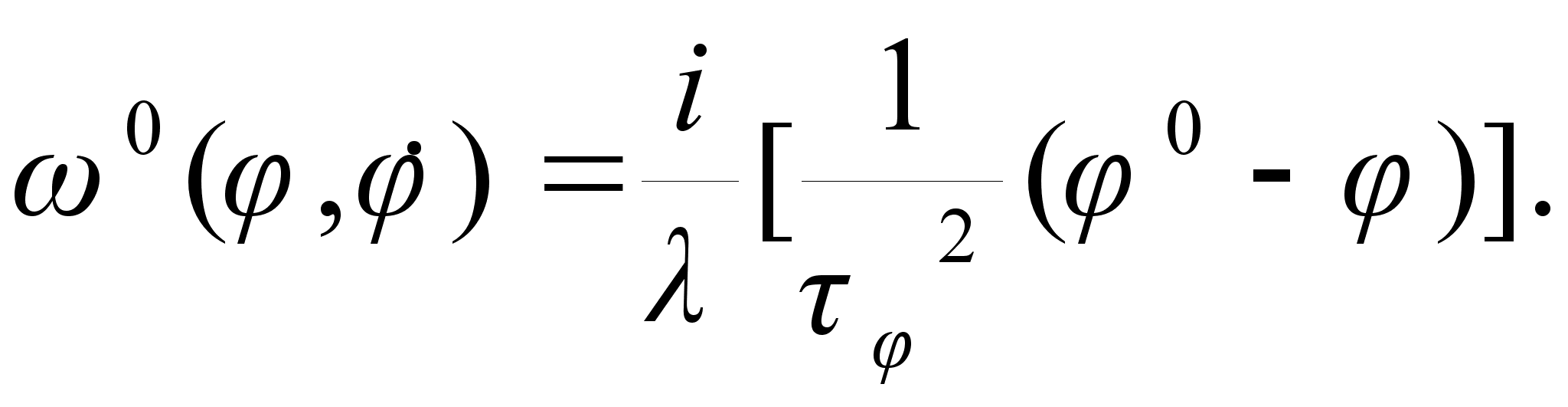
Это уравнение подставим в формулу
