Реферат: Математическое моделирование электропривода

и рассматривают следующие уравнения динамики:

(7)

Эта модель будет использоваться для построения алгоритмов управления угловой скоростью вращения и углом поворота вала двигателя.

Исключим из (7) переменную . Имеем

(8)

Следовательно, управляющее ускорение примет вид

(9)

Задающим воздействием для контура угловой скорости является величина . В установившемся режиме обеспечивается , если и коэффициент усиления . Эти параметры должны быть рассчитаны с учетом электромеханических характеристик двигателя.

Параметр характеризует скорость уменьшения ошибки в соответствии с экспоненциальным законом , где .Величина есть постоянная времени контура угловой скорости. Она должна быть не меньше механической постоянной двигателя. Следовательно

(10)

От сюда видно, что быстродействие контура угловой скорости уменьшается с уменьшением величины . При быстродействие контура предельно.

После определения параметра следует рассчитать значение коэффициента усиления контура ускорения. Исходим из уравнения управляемого процесса по угловой скорости, при

(11)

Согласно принятым обозначениям

поэтому частные производные

(12)

Расчетное соотношение для можно вывести, анализируя динамику контура ускорения. Дифференцируя первое уравнение (11) по времени и подставляя затем в него выражение для из второго уравнения, будем иметь

(13)

где . Это уравнение описывает процессы в контуре ускорения. Постоянная времени , подставляя выражения для частных производных из (12), этого контура равна

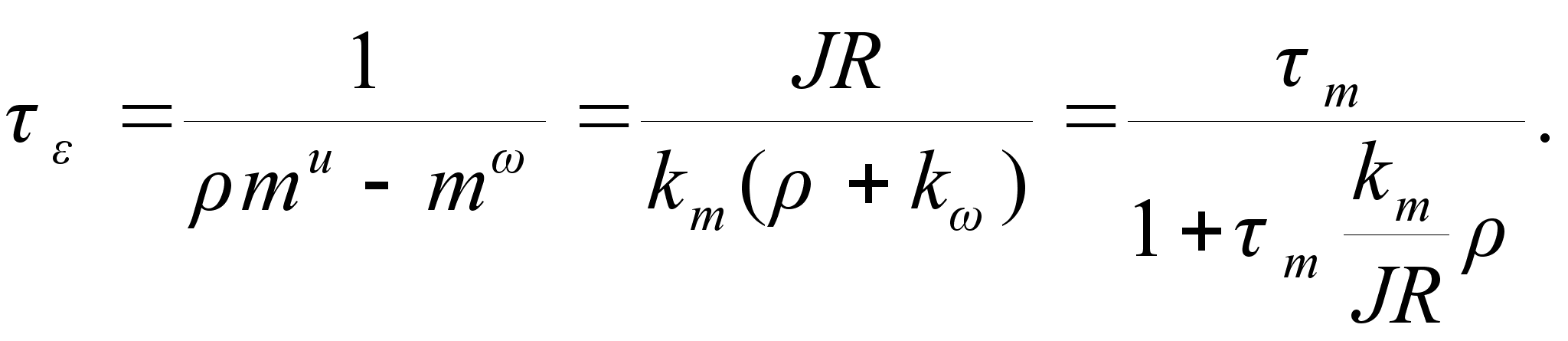(14)

Процесс управления угловой скоростью будет соответствовать назначенному закону, если быстродействие контура ускорения существенно выше контура , т.е. . В свою очередь, величина не может быть назначена произвольно, поскольку управляемый двигатель обладает инерционностью. Нижний предел постоянной времени определяется электрическими свойствами якорной цепи. Действительно из уравнения (6) можно найти

Как видно, скорость изменения ускорения определяется электрической постоянной времени . Отсюда чтобы предъявляемые требования по быстродействию контура ускорения были физически реализуемыми, величина не может быть меньше . Из (14) имеем

(15)

Поскольку то формула (15) всегда дает . В случае реализуется наибольшее быстродействие контура ускорения. Если наряду с этим согласно (10) принимается , то найденные параметры обеспечивают предельное (по физическим возможностям) быстродействие контура обработки угловой скорости. В таком случае по (10) и (15) имеем

(16)

Итак, параметры алгоритма управления угловой скоростью вращения вала двигателя рассчитываются по формулам (10) и (15).

В нашем случае контур управления угловой скоростью может быть построен без измерения ускорения . Для этого управляющую функцию необходимо формировать не по (11), а учитывая что