Реферат: Материальные уравнения Максвелла для биологических объектов

Если к электролиту приложено электрическое поле , то на ионы сорта с зарядом , где - валентность иона, будет действовать сила . Однако ясно, что скорость иона не может возрастать безгранично, поскольку при своём движении он испытывает силу трения, которая пропорциональна его скорости . Эту силу можно представить в виде , где - коэффициент трения. В результате совместного действия электрической силы и силы трения устанавливается стационарное движение иона, при котором

(3.1.2)

где 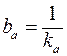- подвижность иона.

Скорость ионов, как правило, невелики, например при поле 1 В/см и температуре 25 градусов С большинство ионов в воде двигаются со скоростью порядка см/c. Исключение составляют ионы водорода, которые могут двигаться со скоростью порядка см/c [19].

Учитывая (3.1.1) и (3.1.2), находим плотность тока, ионов данного сорта:

(3.1.3)

Если в растворе имеется несколько сортов ионов, то суммарный ток определяется суммой парциальных ионных токов из соотношения:

(3.1.4)

В связи с тем, что масса ионов, переносящих ток в электролитах, велика, случае переменного напряжения инерционные свойства ионов могут влиять на перенос тока. Связь ускорения ионов, их массы и прикладываемого к среде электрического поля, имеет вид:

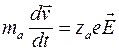, (3.1.5)

где и – масса и заряд иона соответственно, – напряженность электрического поля, – скорость движения заряда.

В данном уравнении считается, что заряд иона отрицательный. Используя соотношение (3.1.1) и (3.1.5), получаем значение плотности ионного тока ионов данного сорта:

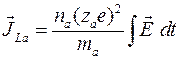. (3.1.6)

Введя обозначение

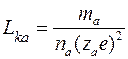, (3.1.7)

где - удельная кинетическая индуктивность ионов данного сорта, получаем

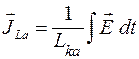. (3.1.8)

Существование кинетической индуктивности связано с тем, что заряд, имея массу, обладает инерционными свойствами. Для случая гармонических полей соотношение (3.1.8) запишется:

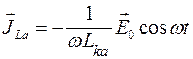. (3.1.9)

Из соотношения (3.1.8) и (3.1.9) видно, что представляет индуктивный ток, т.к. его фаза запаздывает по отношению к напряжённости электрического поля на угол .

Если в электролите находятся разные сорта ионов, то суммарный индуктивный ток запишется как их сумма:

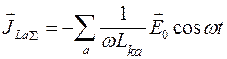(3.1.10)

С учётом соотношений (3.1.4) и (3.1.10) общий ток, текущий через электролит можно записать

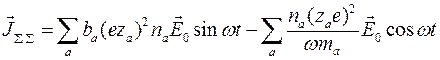(3.1.11)

Полученное соотношение показывает интересную особенность суммарного тока, текущего через электролит. Резистивный ток, представленный первым членом правой части, от частоты не зависит, в то же время индуктивный ток, представленный вторым членом правой части, обратно пропорционален частоте и на низких частотах может существенно превосходить резистивный ток. Это обстоятельство говорит о том, что, работая на низких частотах легко перепутать резистивный и индуктивный ток. Для того чтобы их различать, необходимо измерять разность фаз между прикладываемым электрическим полем и током, текущим через электролит. Таким образом, всегда можно подобрать частоту так, чтобы измерять активную составляющую плотности ионного тока.

3.2. Диэлектрические среды биологических тканей.

В состав биологических тканей входят также молекулы, заряды в которых связаны. Такие молекулы обладают диэлектрическими свойствами и могут поляризоваться в электрических полях.

Если заряды связаны, то они представляют из себя механический осциллятор, который способен резонировать на определённой резонансной частоте .

Рассмотрим простейшую модель электронной поляризации молекул. В этом случае отдельная молекула может быть представлена как механический осциллятор, когда заряд, имеющий массу, под воздействием электрических сил осуществляет вынужденное колебательное движение около центра масс [20]. В этом случае отклонение поляризуемых зарядов от положения равновесия определяется величиной электрического поля и коэффициентом упругости, характеризующего упругость сил связи зарядов в молекулах. Эти величины связаны соотношением