Реферат: Материальные уравнения Максвелла для биологических объектов

где - параметры, первый из которых это отклонение зарядов от положения равновесия, а второй - представляет коэффициентом упругости, характеризующий упругость электрических сил связи зарядов в молекулах. В соотношении (3.2.1) индексом обозначена масса данного сорта молекул.

Вводя резонансную частоту связанных зарядов

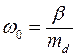, (3.2.2)

из ( 3.2.1) получаем:

(3.2.3)

Видно, что в соотношении (3.2.3) как параметр уже присутствует резонансная частота собственных колебаний, в которую входит масса заряда. Это говорит о том, что инерционные свойства колеблющихся зарядов, подобно индуктивности в колебательном контуре, будут влиять на колебательные процессы поляризуемых атомов и молекул.

. Запишем плотность тока связанную с движением зарядов

(3.2.4)

где - плотность молекул в рассматриваемой среде.

Воспользовавшись соотношением (3.2.3) для нахождения скорости колеблющихся зарядов, получим

. (3.2.5)

Подставляя это выражение в соотношение (3.2.4), находим:

(3.2.6)

или

, (3.2.7)

где - кинетическая индуктивность связанных зарядов.

Видно, что выражение, стоящее перед производной в правой части выражения (3.2.7), играет роль диэлектрической проницаемости среды.

Если в ткани имеются молекулы разных сортов, то для нахождения суммарного тока нужно произвести суммирование всех парциальных токов:

Считая, что напряженность электрического поля изменяется по гармоническому закону , из (8) находим:

(3.2.8)

Теперь, используя соотношения (3.1.11) и (3.2.8), найдём полный ток текущий через биологическую ткань с учётом всех компонент, входящих в её состав:

(3.2.9)

В это соотношение входит три составляющие тока, текущие через

биологическую ткань. Первый член правой части представляет резистивный ток, второй член является индуктивным током, эти оба тока характеризуют ионный ток в межклеточном электролите. Последний член правой части представляет ёмкостные токи, связанные с наличием молекул, в которых заряды связаны.

Следует сказать, что пока за кадром остались те молекулы, которые тоже присутствуют в биологических тканях и которые обладают собственным электрическим дипольным моментом, и поляризация которых связана с поворотом электрических диполей этих молекул вдоль прикладываемого поля. Ясно, что в этом случае вид тока будет соответствовать последнему члену в соотношении (3.2.9), однако как выразить кинетику такого поворота для молекул пока не ясно, тем более что сам поворот будет осуществляться в вязкой среде, а, значит, необходим учёт трения при таком повороте.

Если бы имелась возможность измерить значения всех составляющих тока, входящих в соотношение (3.2.9) и их частотную зависимость, то в нашем распоряжении был бы мощный метод исследования биологических тканей и их паталогий. Однако это очень сложная задача, которая требует применения не только широкого спектра частот, но и методов дистанционного введения этих частот в ткани организма и измерения ответной реакции на такое введение.

4. Постановка задачи и её реализация.

По указанной причине задачей данной работы является пока только разработка методики, которая даёт возможность определять активную составляющую тока межтканевого электролита, при наличии максимальной локализации таких измерений. Максимальная локализация необходима для того, чтобы иметь возможность обнаруживать паталогию тканей минимальных размеров, а также исследовать свойства тканей в переходной области между здоровой тканью и паталогической.

При выборе параметров измерительного устройства на него накладывается целый ряд требований, которые очень часто являются противоречивыми. Например, максимальная локализация измерений означает, что зондирующие поля и токи должны быть сосредоточены в очень малых объёмах, а это означает, что при прямом методе измерения, когда измеряется непосредственное падение напряжения при пропускании токов, в указанной области могут иметь место недопустимо высокие уровни рассеиваемой мощности, которые сами по себе будут влиять на результаты измерений, поскольку будут разогревать область измерений. Более того, измерение напряжения и тока даже в приборах первого класса осуществляется всего до второго, в лучшем случае, третьего знака для обычных значений напряжений. Если же нужно измерять микровольты и микроамперы, то погрешность оказывается гораздо выше. По этой причине очень желательно использование частотного метода измерения, когда полученная информация преобразуется в частоту, которая может быть простыми средствами измерена до шестого седьмого знака. По этой причине в качества датчика выбран резонансный контур, в котором параллельно основной ёмкости подключена дополнительная ёмкость, последовательно с которой включается резистивный участок исследуемой биологической ткани. Используя метод векторных диаграмм нетрудно показать, что резонансная частота такого контура будет зависеть от активного сопротивления исследуемого участка ткани. По причине ограниченности объёма курсового проекта мы не будем останавливаться на этом непринципиальном вопросе, укажем лишь то, что на практике этот вопрос решается очень просто путём калибровки.