Реферат: Метод статистической стабилизации частот независимо функционирующих генераторов

Как отмечалось ранее, случайные величины являются независимыми и имеют известные параметры распределения (математическое ожидание, медиана или дисперсия). В силу этого плотность распределения (1) случайных величин для каждого момента времени может быть записана в виде (3).

С учетом этого можно отметить, что случайные величины являются независимыми и удовлетворяют нормальному закону распределения с математическим ожиданием, равным нулю:

.(12)

Запишем формулу для плотности нормального закона распределения величины :

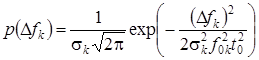,(13)

где – относительная нестабильность k -го генератора .

Величины отклонений частот связаны с нестабильностью временного интервала соотношением (8), что позволяет использовать для оценки нестабильности временного интервала метод наибольшего правдоподобия. В соответствии с данным методом составим функцию наибольшего правдоподобия относительно неизвестного значения отклонения длительности временного интервала :

. (14)

После подставки выражения (8) в (14) и получим следующее выражение относительно переменной :

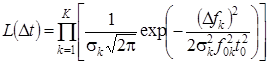.(15)

После логарифмирования данной функции получаем:

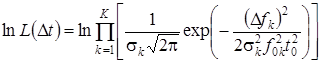,(16)

или с учетом свойства логарифмической функции

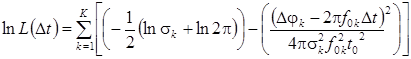. (17)

В соответствии с методом наибольшего правдоподобия продифференцируем данную функцию, что позволит получить равенство:

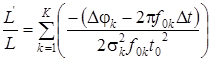. (18)

В качестве оценки нестабильности временного интервала берется такое значение параметра , при котором производная (17) обращается в нуль. Приравняем данное выражение к нулю, что позволяет получить:

. (19)

Выразим из данного выражения оценку отклонения длительности временного интервала измерений от номинального значения :

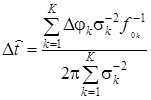. (20)

Полученное значение определяет стационарную точку функции (17). Для того чтобы доказать наличие экстремума, с помощью равенства (18) вычислим вторую производную и оценим выполнение второго достаточного условия локального экстремума:

.

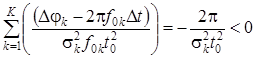Исходя из того, что вторая производная функции правдоподобия меньше нуля, функция правдоподобия при значении , определяемом (20), действительно достигает максимума.

Соотношение (19) является необходимым условием локального экстремума функции правдоподобия. В то же время исходя из того, что функция (19) относительно аргумента является квадратичной, можно утверждать, что данный экстремум будет глобальным.

Найденная оценка нестабильности временного интервала позволяет вычислить составляющую для каждого генератора и разделить две составляющие и , определяющие соответственно вклад собственной нестабильности k -го генератора и нестабильности временного интервала измерений в измеренное значение .

Для этого значение подставим в формулу (11) и найдем оценки нестабильности частот каждого из совокупности генераторов, получаемые на основе измеренных значений и полученной с использованием выражения (20) оценки нестабильности временного интервала.

Найденные значения позволяют определить отклонения частот генераторов в виде:

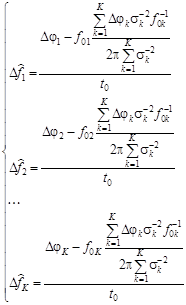.(21)

Полученные оценки позволяют по измеренным значениям числа импульсов или фаз колебаний каждого из совокупности генераторов и их номинальным значениям определить, на какую величину отличается частота каждого генератора от своего номинального значения. Это дает возможность по результатам измерений и последующей обработки формировать управляющие сигналы для уменьшения отклонения частоты каждого из совокупности генераторов от номинальных значений.