Реферат: Метод Винера-Хопфа и его приложения в физических задачах

Демидов Р.А. ,ФТФ, 2105

Введение

Указанный метод подходит для решения интегральных уравнений на полубесконечном промежутке с ядром, зависящим от разности аргументов – речь идет об уравнениях вида

.

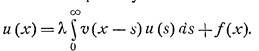Этот метод был предложен в совместной работе Н.Винера и Э.Хопфа в 1931 году, и находит разнообразные применения в теории дифференциальных и интегральных уравнений, а также в их приложениях в физических задачах.

В своей работе я опишу сам метод Винера-Хопфа, а также приведу его применение к решению краевых задач матфизики.

1. Метод

1.1 Случай бесконечного промежутка

Метод Винера-Хопфа основан на специальном виде ядра интегрального уравнения – оно зависит от разности аргументов, а не от самого аргумента. Собственно, для начала рассмотрим уравнение вида

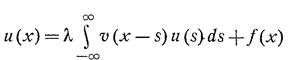⁽¹⁾

- это уравнение с бесконечным промежутком и тем же самым ядром. Решение его существует ,если выполняются 2 условия:

,

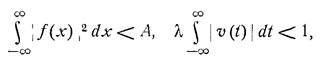а также условие сходимости нормы u(x):

.

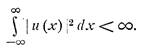Эти условия работают при действительных λ. Мы рассмотрим два способа решения этого уравнения – один, использующий свойство свертки напрямую, другой – с помощью резольвенты. Итак,первый .Заметим, что в случае именно бесконечного промежутка интеграл представляет собой свертку ядра и функции u(x). Вспомнив,что Фурье-образы функций u(x),f(x),g(x) выглядят как, воспользуемся свойством образа свертки двух функций – “образ свертки есть свертка образов”. Тогда для функций U(k),V(k),F(k) – образов соответствующих функций, получаем алгебраическое уравнение:

⁽²⁾

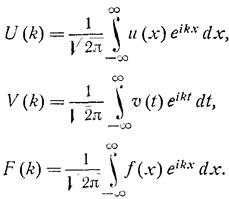
Данное свойство образа свертки доказывается “в лоб”, а именно – домножением равенства (1) на 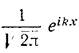и интегрированием по всей действительной оси:

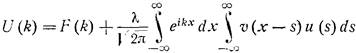
Делая замену во втором интеграле (x-s)=t, получаем

,

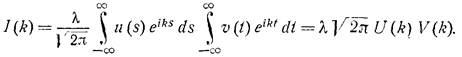что и требовалось доказать.

Видим, что мы свели исходную задачу к алгебраическому уравнению относительно образа исходной функции u(x). Выражая его через образы ядра и f(x),производя обратное преобразование Фурье, получаем в качестве искомого решения:

=>

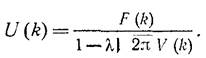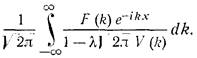=> ⁽³⁾

Второй способ: вычисляем резольвенту уравнения как

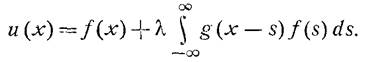⁽⁴⁾

В виде Фурье - образов это равенство выглядит так:

,

где G(k) вычисляется как

--> ЧИТАТЬ ПОЛНОСТЬЮ <--