Реферат: Метод Винера-Хопфа и его приложения в физических задачах

V(k) – Фурье-образ исходного ядра v(x) уравнения (1).То есть для решения исходного уравнения необходимо найти функцию g(x),применив обратное преобразование Фурье к (5),и подставить его в (4). Этот способ не требует вычисления каждый раз интегралов для F(k) при смене функции f,она подставляется в самом конце один раз, поэтому такой способ быстрее.

На примере этой задачи мы поняли, как решать уравнение с бесконечным промежутком интегрирования. На этом примере мы будем строить решение уравнения с полубесконечным промежутком – и опишем метод Винера-Хопфа.

1.2 Полубесконечный промежуток

Понятно, что в случае, если интегрирование идет не с -∞, а с 0, переходя к образам, мы не можем воспринимать наш интеграл как свертку – а значит, и не можем написать наше уравнение. Запишем некоторые свойства преобразования Фурье, связанные с полубесконечными промежутками, которые нам понадобятся в дальнейшем. Итак, в случае разбиения функции f (x) на два куска – f₊ (x) и f_- (x), (f(x)= f₊ (x) + f_- (x) )представляющих собой правый и левый концы следующим образом:

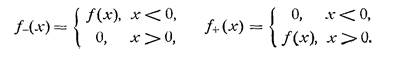
выражения для прямых и обратных преобразований Фурье для них будет выглядеть так:

f₊ ^: ,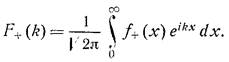

при причем здесь - комплексная переменная, и выполняется неравенство Im(k)=τ > τ_{- .} Причем

Обратное преобразование выглядит так:

,

и здесь мы интегрируем по любой прямой Im(k)=τ > τ_- .

f_- ^: При

для прямого преобразования Фурье имеем

,

к здесь та же к.п. ,это верно в области с Im(k)=τ < τ_{+ .} Обратное преобразование для f_- выглядит аналогично:

Интегрирование идет по той же прямой с Im(k)=τ < τ₊

При τ_- < τ₊ образ F(k) задаётся уравнением

как раз в полосе τ_- < Im(τ) < τ_{+ .} При τ_- < 0,τ₊ > 0 функция полоса Im(τ)=0 попадает в границы интегрирования, и интеграл можно взять вещественным, выбрав мнимую часть τ нулем.

Применим эти соображения к решению искомого уравнения. (6)

⁽⁶⁾

Разложим неизвестную функцию u(x) на составляющие u₊ , u_- :

При подстановке этих функций в уравнение (6) мы получаем два уравнения на каждую часть u(x).Факт существование решения мы примем без доказательств. Мы ищем решения, удовлетворяющие следующим условиям:

,

µ<τ₊ .

При их выполнении в полосе µ < Im(k) < τ₊ функции u₊ ,u_- являются аналитическими.