Реферат: Метод Винера-Хопфа и его приложения в физических задачах

Условия на границы по мнимой оси для функций Ф₊ ,Ф_- сохранятся => лемма доказана.

Теперь сделаем еще одно обобщение – покажем, как в общих чертах работает этот метод для неоднородного уравнения

⁽⁷⁾

Проводя аналогичные рассуждения, разбивая u(x) на две вспомогательные функции, замечаем, что при выполнении условий для модуля

в полосе мы можем переходить к образам функций и мы получим

предварительно разбив F на две. Принимая за функцию L(x) ф-ю

,

аналитическую в стандартной полосе и равномерно стремящуюся к 1 при наше алгебраическое уравнение перепишется как

Далее, точно также разделяем L на две части как

,

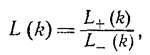И L₊ - аналитическая в , L_- - аналитическая в . По аналогии приводя к общему знаменателю, получаем уравнение на U₊ ,U_- :

При успешном разложении последнего члена как

,

где по все той же аналогии D₊ и D_- аналитические в областях соответственно, мы записываем решения в виде

.

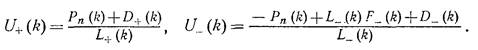При этом мы воспользовались той же сходимостью – L₊ ,L_- растут не быстрее чем kⁿ , а значит, для выполнения условий необходим полином в числителе.

Как видим, и эта, неоднородная задача, успешно решилась методом Винера-Хопфа. Как таковой, метод основан на некой аналогии разделения переменных – мы разделяем одну функцию на сумму двух, каждая из которых закрывает свою зону комплексной плоскости, и с каждой половиной работаем отдельно.

Метод мы рассмотрели, поняли, как он работает, теперь рассмотрим его конкретное применение – в краевых задачах математической физики.

2. Применение метода Винера-Хопфа

До этого мы рассматривали наш метод для решения интегральных уравнений, однородных и неоднородных, с специальным ядром. Сейчас же рассмотрим уравнение Лапласа и краевую задачу на нем, тем самым обобщив м. В.-Х. и на дифференциальные уравнения в частных производных.

Итак, задача: в верхней полуплоскости найти гармоническую функцию, удовлетворяющую следующим условиям:

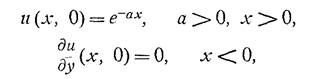
Для этого решим к. задачу на уравнении , ,и перейдем уже в решении к пределу в нуле по каппа.

Разделяя переменные, и применяя метод Фурье, в общем виде находим решение:

,
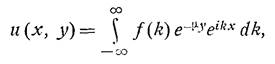