Реферат: Моделі управління запасами в прийнятті управлінського рішення

У цій формулі q - визначає розмір партії продукції і за аналогією з попередньою задачею ТС одержує мінімальне значення, якщо

q_о = 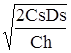. (8.8)

Одержана за формулою оптимальна кількість продукції в партії називається економічним розміром партії (ЕОQ). Модель цієї партії надана на рис. 8.6.

Рис. 8.6 - Модель економічного розміру партії

Розрахунки за моделлю можна проілюструвати прикладом компанії, яка виробляє з кераміки декілька видів сантехнічних виробів. Виробничий процес організований за принципом випуску 500 штук виробів за тиждень. Попит па популярну модель складає 12500 виробів на рік і рівномірно розподіляється протягом року. Вартість наладки виробничого процесу па партію складає 200 грн., а вартість зберігання виробів - 1,5 грн за одиницю.

Треба визначити оптимальну партію випуску виробів, частоту поновлення виробничого циклу та його тривалість.

Економічний розмір партії виробництва виробів можна визначити за формулою (8.8)

q_о = = .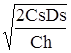

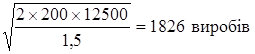Отже за оптимальний розмір партії можливо прийняти 1800 виробів.

Тоді число виробничих циклів за рік складає:

12500: 1820 = 6,97,

інтервал між циклами дорівнює

1800 ? 52 / 12500 = 7,5 тижнів,

а процес виробництва однієї партії при обсязі тижневого випуску 500 виробів займе 1800 / 500 = 3,6 тижня.

В інтервалах між виробничими циклами компанія планує партії інших виробів.

Вплив знижок на розмір замовлення

У багатьох компаніях і товариствах при замовленні збільшеного розміру поставок установлені знижки з оптової ціни. Замовляючи партії поставок більші від оптимального розміру, підприємство ризикує збільшенням вартості запасів. Проте воно може бути компенсоване зниженням закупівельної ціни.

Загальна вартість закупки та запасів (М) з урахуванням знижок визначається так:

М = Со (D / q) + Сh ? (q/2) + СD. (8.9)

Якщо закупівельна ціна постійна і не залежить від розміру замовлення, включення вартості закупленої продукції (СD) у рівняння загальної вартості приводить до переміщення цього рівняння паралельно осі без зміни її форми. При цьому критична точка оптимального замовлення (ЕОQ) не переміщується (рис. 9.3).

Якщо товар реалізується за ціною С за одиницю, але для замовлень, розмір яких перевищує певну величину q _І , надається знижка, відповідно до якої ціна за одиницю продукції знижується до величини С_І ,. змінюється крива загальної вартості. При цьому розмір замовлення q_І може перевищувати оптимальний q₀ . Але для прийняття рішення про розмір замовлення треба провести відповідні розрахунки,

Знижка може бути прогресивною, тобто збільшуватися при подальшому зростанні розміру разового замовлення. Тому треба провести розрахунки загальної вартості по кожному варіанту ціни.

Для ілюстрації розрахунків використаємо попередній приклад. Підприємство одержує в рік D = 4000 одиниць продукції за ціною С = 500 гривень. Вартість зберігання одиниці запасів Сh = 600 грн., а вартість подачі одного замовлення Со = 1200 грн. Оптимальний розмір замовлення в цих умовах складає ЕОQ = 126,5 одиниць при сукупних витратах на зберігання ТС = 75894,66 грн.

За умовами поставки надається знижка 4%, якщо рівень замовлення знаходиться в межах 200 - 499 одиниць і в розмірі 6%, якщо рівень замовлення становить 500 і більше одиниць (табл.9.2).

Виходячи з цих умов, слід перевірити доцільність використання знижок. При цьому враховується, що зі збільшенням розміру замовлення вартість продукції на одиницю зменшиться, знизиться також вартість замовлення, але зростуть витрати на зберігання.

У початковому варіанті загальна вартість закупки та запасів (М) складає:

М₁ = 37944,66 + 37950 + 2000000 = 2075894.66грн.

Таблиця 8.2 - Знижки з ціни за одиницю продукції залежно від розміру замовлення

Розмір замовлення	Знижка, %	ЦінЦіна за одиницю, грн.
0-199	0	500
200 - 499	4	480
500 і більше	6	470